Question

найти площадь фигуры ограниченной линиями y=2+x^2 y=3

Answer 1

S = 10 2/3

Объяснение:

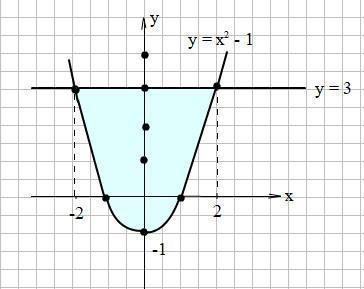
Смотри рисунок на прикреплённом фото.

Найдём пределы интегрирования.

х² - 1 = 3

х² = 4

х = ±2

верхний предел х = 2, нижний предел х = -2

По графику видно, что в этих пределах у = 3 расположена выше у = х²-1

S = ₋₂∫²(3 - (x² - 1)) dx = ₋₂∫²(4 - x²) dx = (4x - x³/3)₋₂ /⁺² =

=8 - 8/3 - (-8 + 8/3) = 16 - 16/3 = 16 · 2/3 = 32/3 = 10 2/3