Предмет: Алгебра,
автор: vityamath
при каких значениях параметра a уравнение

имеет единственный корень???
Ответы
Автор ответа:
2
Ответ:
(см. объяснение)
Объяснение:
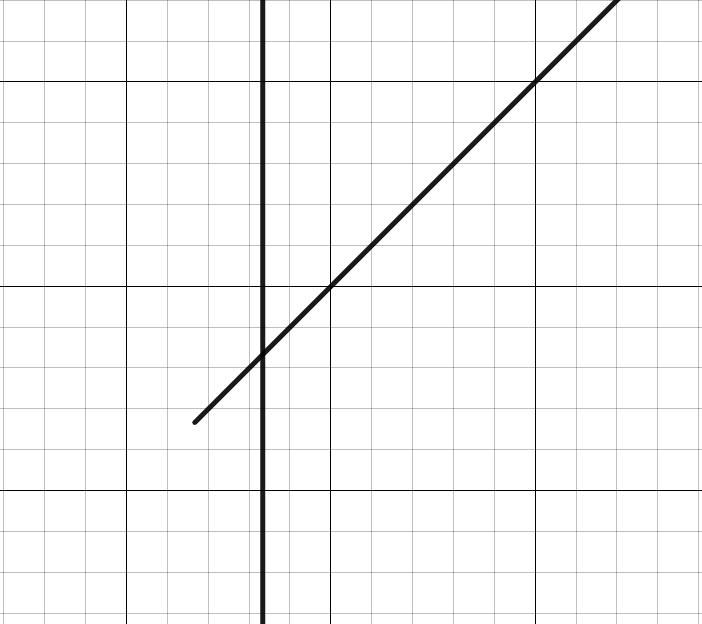
Графический метод:
Строим графики (прямая) и
(
) при
, откуда видим, что ответом будет
.
(см. прикрепленный файл)
Аналитический метод:
, ОДЗ:
.
Заметим, что при любом значении параметра исходное уравнение имеет корень .
Тогда один корень у такого уравнения будет, если:
- Первый множитель тоже обращается в 0 при
.
- Он обращается в 0 при x, который не подойдет по ОДЗ.
В первом случае при подстановке в числа
вместо x получаем, что
. Действительно, в этом случае корень единственный.
Во втором случае имеем, что . ОДЗ нарушается, если
, то есть тогда
.
Итого при исходное уравнение имеет ровно один единственный корень.
Задание выполнено!
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Окружающий мир,
автор: ННастянн
Предмет: Английский язык,
автор: Настёна151
Предмет: Физика,
автор: muxalelya
Предмет: Алгебра,
автор: Николай123334444