Question

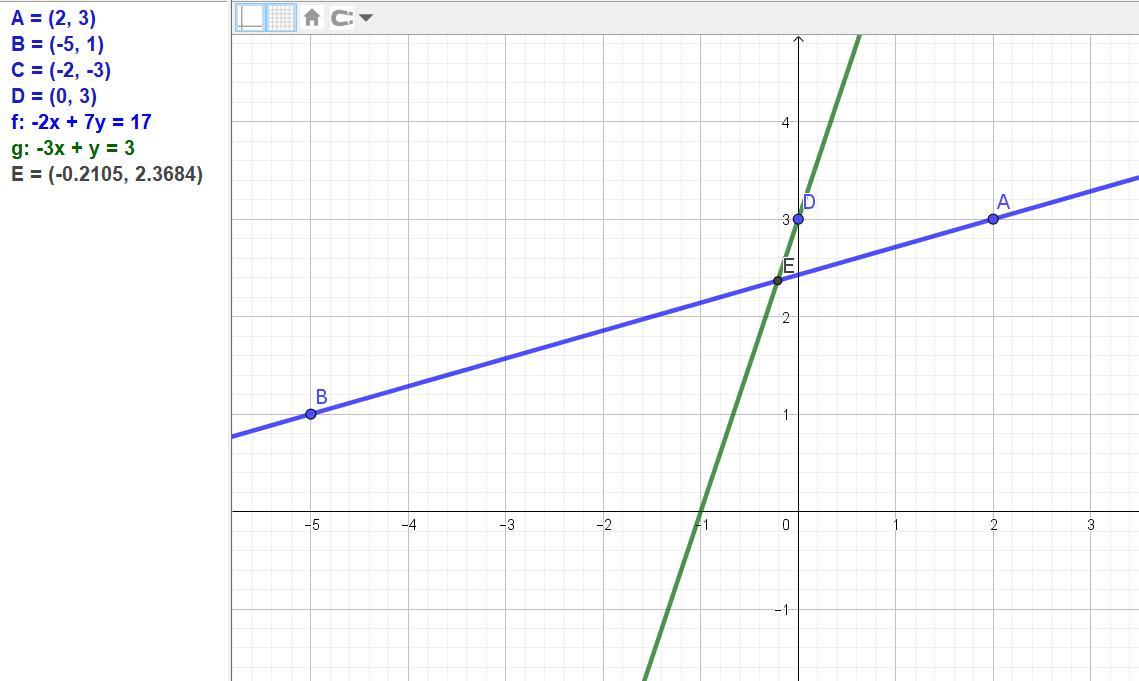
1) Написать уравнения AB и CD, если известны координаты точек
2) Найти координаты точки пересечения этих прямых
3) Определить угловые коэффициенты этих прямых
A:(2;3) ;B:(-5;1) ;C:(-2;-3) ;D:(0;3)

Answer 1

Даны точки A(2;3); B(-5;1); C(-2;-3); D(0;3).

1) Находим векторы АВ и CD.

AB = (-5-2; 1-3) = (-7; -2).

CD = (0-(-2); 3-(-3)) = (2; 6).

Уравнения:

AB: (x - 2)/(-7) = (y - 3)/(-2)      каноническое.

     -2x + 4 = -7y + 21,

     2x - 7y + 17 = 0,               общее,

     y = (2x + 17)/7 или

     y = (2/7)x  + (17/7)              с угловым коэффициентом.

CD: (x + 2)/2 = (y + 3)/6,

       6x + 12 = 2y + 6,

       6x - 2y + 6 = 0,

       3x - y + 3 = 0.

       y = 3x + 3.

2) Надо решить систему:

   2x - 7y + 17 = 0|x3 =   6x - 21y + 51 = 0

    3x - y + 3 = 0|x (-2) = -6x + 2y - 6 = 0    

                                             -19y + 45 = 0, y = 45/19 ≈ 2,3684,

        x = (y - 3)/3 = ( (45/19) - 3)/3 = (45 - 57)/(19*3) = -12/57 ≈ -0,2105.

3) Угловые коэффициенты прямых определены в пункте 1).

АВ: к = 2/7,

CD: k = 3.