Предмет: Геометрия,
автор: lashkis52
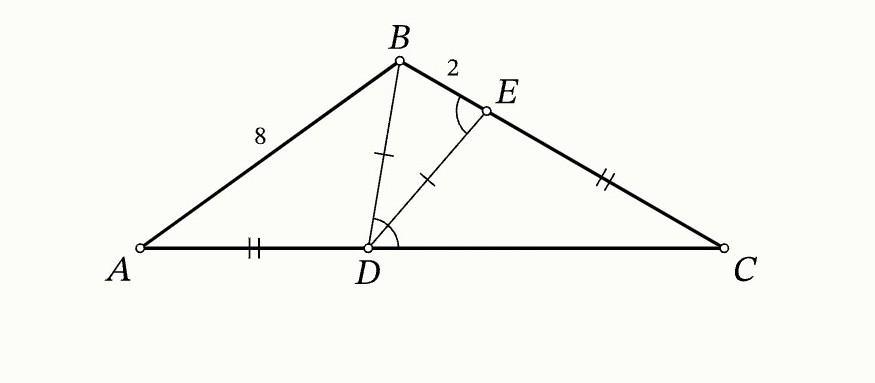
Точки D и E отмечены соответственно на сторонах AC и BC треугольника ABC так, что AD=EC. Оказалось, что BD=ED, ∠BDC=∠DEB. Найдите длину отрезка AC, если известно, что AB=8 и BE=2.
Приложения:
Ответы
Автор ответа:
1
Ответ:13 (ед. длины).
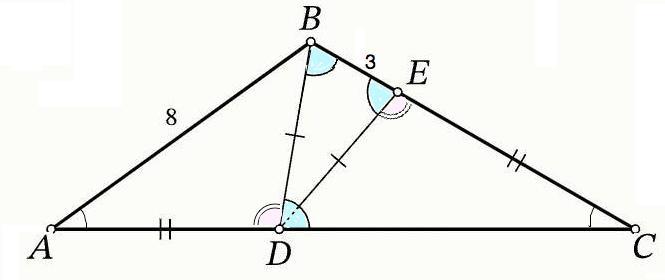
Объяснение: ВD=ED =>∆ BDE – равнобедренный, ∠DBE=∠BED.
Тогда ∆ BCD тоже равнобедренный, т.к. угол ∠BDC=∠DEB. =>
∆ BCD~∆ BDE по равным углам при основаниях. Отсюда следует равенство углов, смежных углам при основаниях этих треугольников. ∠СЕD=∠АDB.
AD=EC, BD=ED. Две стороны и угол между ними ∆ ADB равны двум сторонам и углу между ними ∆ DEC.
∆ СЕD=∆ АDB по 1-му признаку равенства =>
∠BAD=∠BCD. Углы при основании ∆ АВС равны, ∆ АВС - равнобедренный, ВС=АВ=8. =>
СЕ=ВС-ВЕ=8-3=5
АС=AD+DC.
DC=EC=5
AС=5+8=13 (ед. длины).
Приложения:
TheKopoJlb1:
Привет, помоги мне с геометрией пожалуйста.
Похожие вопросы
Предмет: Русский язык,
автор: nikolay123098
Предмет: Русский язык,
автор: lenavlasova191
Предмет: Русский язык,
автор: Аноним
Предмет: Алгебра,
автор: hsnxnxbx
Предмет: География,
автор: polevaia