Предмет: Алгебра,
автор: doritozzz
Помогите пожалуйста
Приложения:
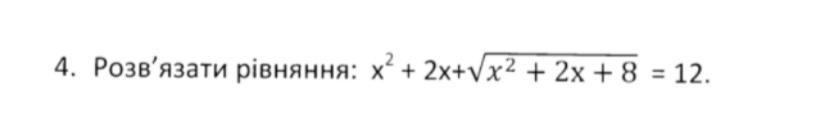
Ответы
Автор ответа:
1
Ответ:
Объяснение:
⇒ x ∈ R
уравнение равносильно
Пусть , тогда уравнение равносильно
квадратному уравнению
неотрицательным корнем которого является число 4.
Следовательно, исходное уравнение равносильно уравнению
О т в е т :
Похожие вопросы
Предмет: Қазақ тiлi,
автор: танш
Предмет: Английский язык,
автор: irissska2
Предмет: Русский язык,
автор: odintsova60
Предмет: Математика,
автор: ulacat
Предмет: Немецкий язык,
автор: Аноним