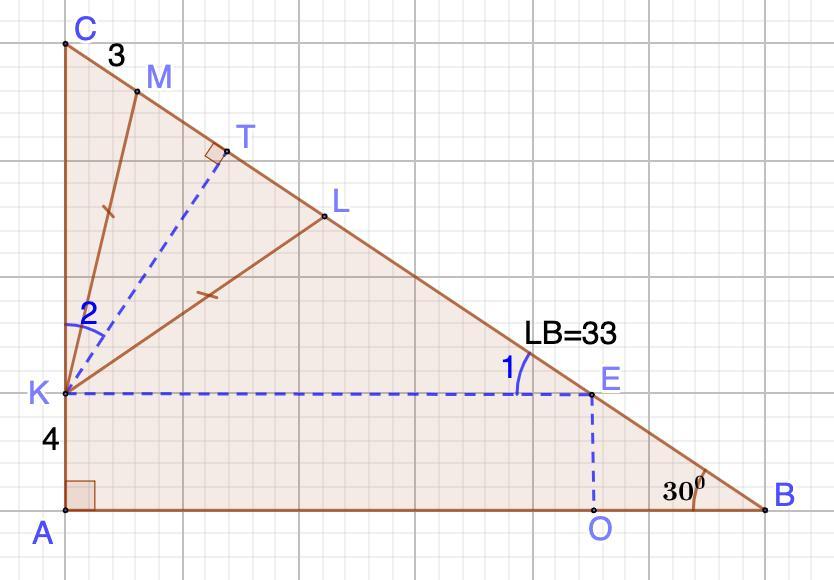
треугольнике ABC известны углы ∠B=30∘ и ∠A=90∘. На стороне AC отмечена точка K, а на стороне BC — точки L и M так, что KL=KM (точка L лежит на отрезке BM). Найдите длину отрезка LM, если известно, что AK=4, BL=33, MC=3.

Ответы
Ответ:
16 ед.
Объяснение:
Дано: ΔАВС - прямоугольный.
∠В=30°
КL=КМ
АК=4; ВL=33; МС=3.
Найти: LМ
Решение:
Дополнительное построение:
КЕ || АВ; ЕО⊥АВ ⇒ АКЕО - прямоугольник.
КТ - высота ΔКМL
Вспомним:
(1) Катет, лежащий против угла 30°, равен половине гипотенузы.
(2) Сумма острых углов прямоугольного треугольника равна 90°.
1.
Рассмотрим ΔОЕВ - прямоугольный (построение)
Противоположные стороны прямоугольника равны.
⇒ ОЕ=АК=4
ЕВ=2ОЕ=8 (1)
⇒ LЕ=33-8=25
2.
Рассмотрим ΔКМL - равнобедренный (условие)
Высота, проведенная к основанию равнобедренного треугольника, является медианой.
⇒ КТ - высота, медиана.
Пусть МТ=ТL=х
⇒МL=2х
3.
Рассмотрим ΔКСЕ - прямоугольный (построение)
∠1=∠В=30° (соответственные при КЕ || АВ и секущей СВ)
СЕ=СМ+МL+LЕ=3+2х+25=28+2х
СК=СЕ:2=(28+2х):2=14+х (1)
4.
Рассмотрим ΔКСТ - прямоугольный (построение)
СТ=СМ+МТ=3+х
∠С=90°-∠В=90°-30°=60° (2)
⇒ ∠2=90°-∠С=90°-60°=30° (2)
СК=2СТ=2·(3+х)=6+2х
5.
СК=14+х (п.3)
СК=6+2х (п.4)
⇒ 14+х=6+2х
х=8
⇒ МL=2x=16