Question

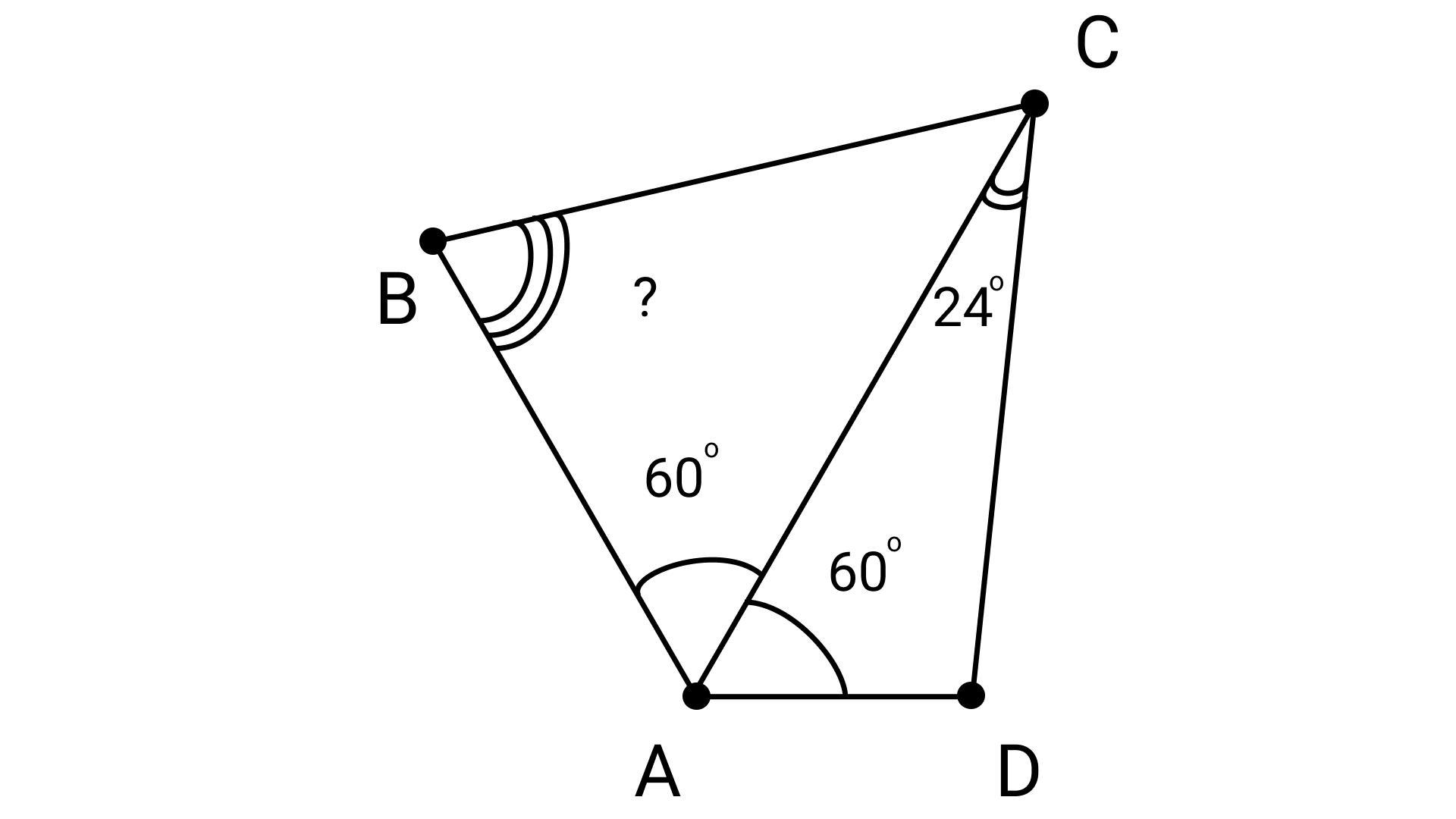
Про четырехугольник ABCD известно, что ∠BAC=∠CAD=60∘, AB+AD=AC. Также известно, что ∠ACD=24∘. Сколько градусов составляет угол ABC?

Answer 1

Ответ:

84°

Объяснение:

Дано: АВСD - четырехугольник;

∠BAC=∠CAD=60°; ∠ACD=24;

AB+AD=AC.

Найти: ∠АВС

Решение:

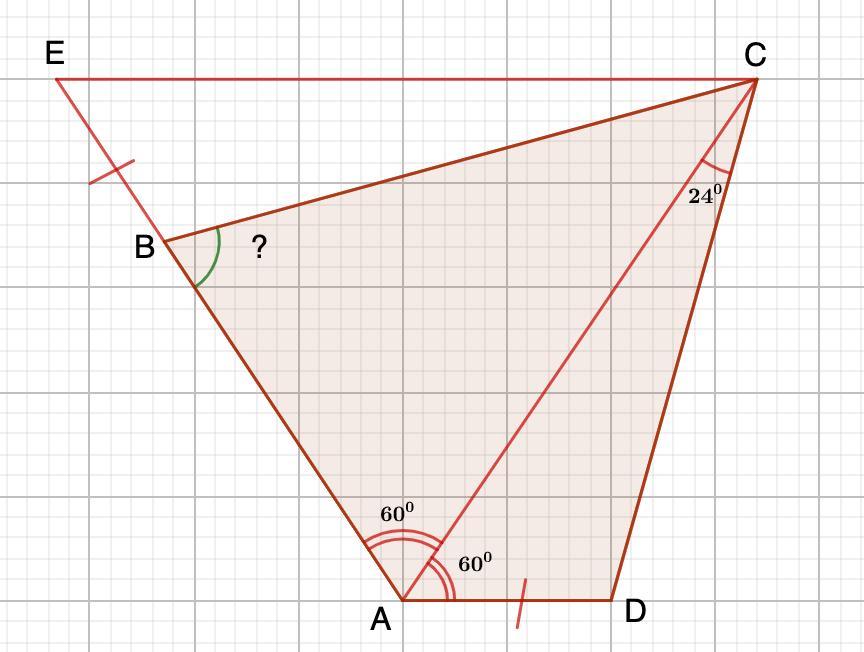
Продлим сторону АВ на отрезок ВЕ=АD.

1. Рассмотрим ΔАЕС.

AB+AD=AC

АВ+ВЕ=АЕ

Так как АD=ВЕ (по построению), то

АС=ВЕ

⇒ ΔАЕС - равнобедренный.

• Углы при основании равнобедренного треугольника равны.

⇒ ∠АСЕ=∠АЕС.

• Сумма углов треугольника равна 180°.

⇒ ∠АСЕ=∠АЕС=(180°-∠ЕАС):2=(180°-60°):2=60°

⇒ ΔАЕС - равносторонний ⇒ АЕ=ЕС=АС

2. Рассмотрим ΔВЕС и ΔАСD.

АС=ЕС (п.1); АD=ВЕ (построение)

∠САD=∠АЕС=60° (п.1)

⇒ ΔВЕС и ΔАСD (по 1 признаку)

∠ЕСВ=∠АСD=24° (как соответственные элементы)

3. Рассмотрим ΔВЕС.

• Сумма углов треугольника равна 180°.

⇒∠ЕВС=180°-(∠ВЕС+∠ЕСВ)=180°-(60°+24°)=96°

• Сумма смежных углов равна 180°.

⇒ ∠АВС=180°-∠ЕВС=180°-96°=84° (смежные)