помогите мне пожалуйста срочно прошу дам 40 баллов за лучший ответ
Ответы
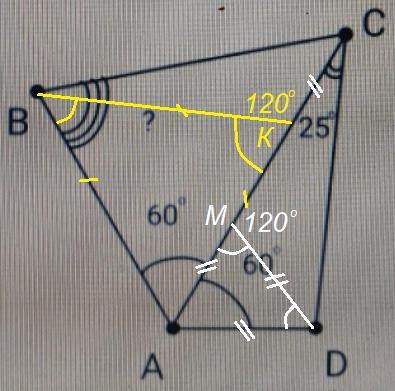
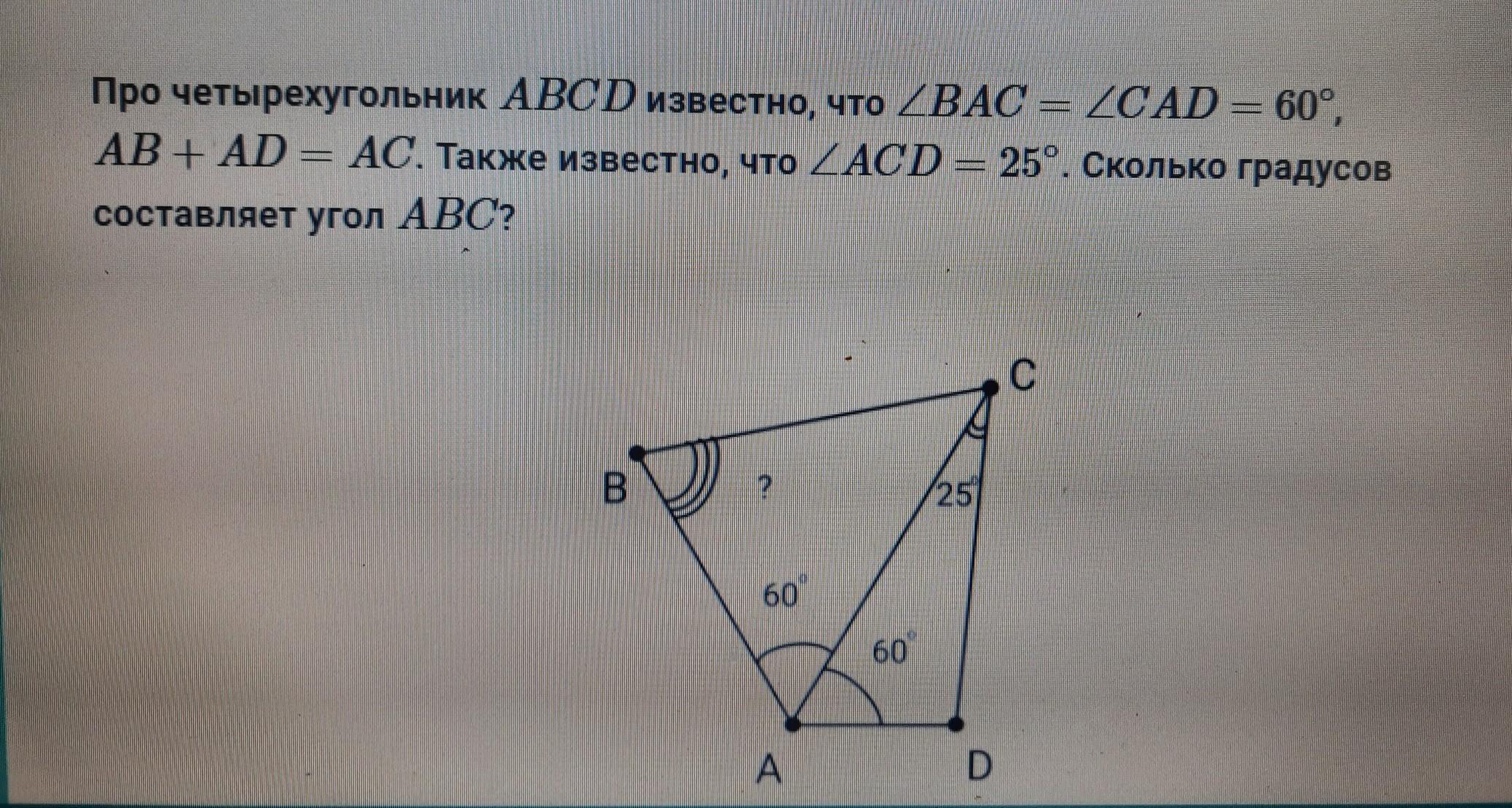
Про четырёхугольник ABCD известно, что ∠BAC = ∠CAD = 60°; AB + AD = AC. Также известно, что ∠ACD = 25°. Сколько градусов составляет угол ABC?
Дано: ABCD - четырёхугольник, ∠ACD = 25°;
∠BAC = ∠CAD = 60°; AB + AD = AC.
Найти: ∠ABC.
Решение:
Так как AB + AD = AC, разобьём отрезок AC точкой К так, что
AK = AB; KC = AD.
Проведём отрезок BK.
Тогда треугольник ABK равнобедренный (AK=AB) с углом при вершине 60° (∠BAK=60°). Значит, этот треугольник равносторонний:
∠BAK = ∠ABK = ∠BKA = 60°
AB = AK = BK
Угол BKC смежный углу BKA=60°, ∠BKC = 120°.
Так как AB + AD = AC, разобьём отрезок AC точкой M так, что
AM = AD; MC = AB.
Проведём отрезок DM.
Тогда треугольник ADM равнобедренный (AD=AM) с углом при вершине 60° (∠MAD=60°). Значит, этот треугольник равносторонний:
∠MAD = ∠MDA = ∠AMD = 60°
AD = AM = DM
Угол DMC смежный углу AMD=60°, ∠DMC = 120°.
ΔBKC = ΔCMD по двум сторонам (KC=DM; BK=MC) и углу между ними
(∠BKC=∠DMC=120°).
Значит, ∠CBK = ∠DCM = 25° как углы, лежащие в равных треугольниках против равных сторон.
∠ABC = ∠ABK + ∠CBK = 60° + 25° = 85°
Ответ: ∠ABC = 85°.