Предмет: Математика,
автор: Iove8
Решите уравнения*** в 213 (***ВАЖНАЯ ПОМЕТКА:Сделали замену и обратно к ней возвращаемся+вычислите дискриминант+уравнение для решения этих* уравнений.(ПРОСБА НЕУДАЛЯТЬ Т.К Я УКАЗАЛ 1 ЗАДАНИЕ¡¡!!)
Приложения:
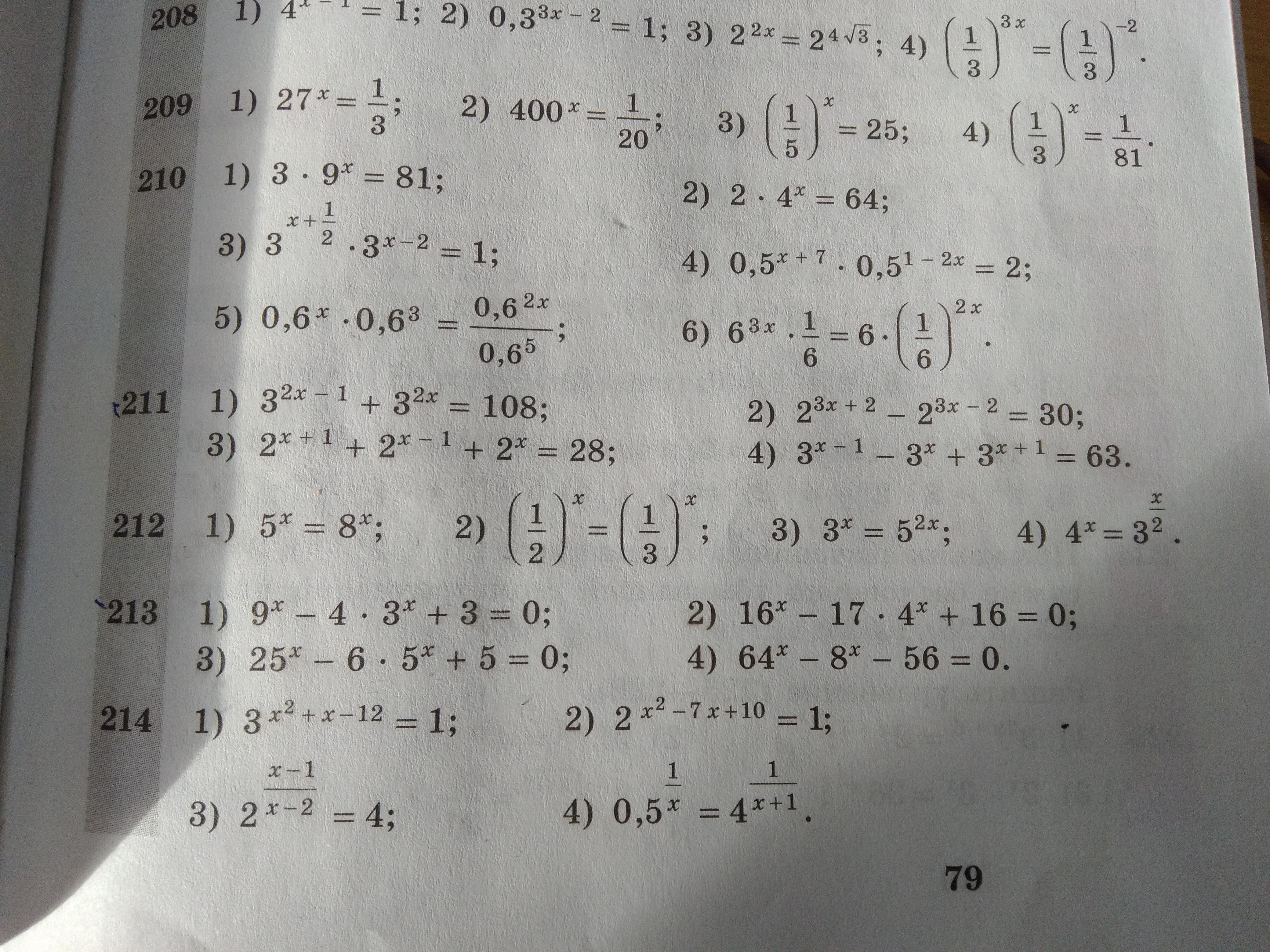
natalyabryukhova:
где?
Ответы
Автор ответа:
0
1)
Пусть , тогда
Подставляем,
;
Ответ: 0; 1
2)
Пусть , тогда
Подставляем,
;
Ответ: 0; 2
3)
Пусть , тогда
Подставляем,
;
Ответ: 0; 1
4)
Пусть , тогда
Подставляем,
;
положительное число при возведении в степень не может стать отрицательным числом, решения у данного уравнения нет.
Ответ: 1
Похожие вопросы
Предмет: Окружающий мир,
автор: воротницкая
Предмет: Окружающий мир,
автор: Асвальт
Предмет: Английский язык,
автор: цветочек53
Предмет: Математика,
автор: Alyosha30
Предмет: Математика,
автор: надежда428