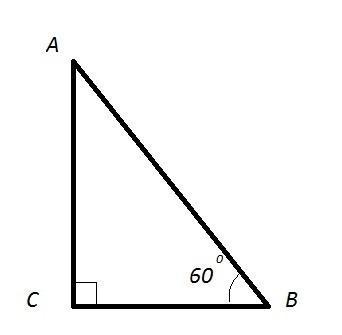
Площадь прямоугольного треугольника равна 18 корней из 3 Один из острых углов равен 60°. Найдите длину катета, лежащего напротив этого угла.
Ответы
Ответ:
ΔАСВ - прямоугольный : АВ - гипотенуза ; АС,СВ - катеты
∠С= 90°
∠В = 60°
Сумма острых углов прямоугольного треугольника равна 90°.
Следовательно: ∠А = 90 - 60 = 30°
Катет лежащий против угла в 30° равен половине гипотенузы.
СВ = АВ/2
По теореме Пифагора:
АВ² = АС² + СВ² ⇒ АВ² = АС² + (АВ/2)²
АС= √ (АВ² - (АВ²/4)) ⇒ АС = √ ((4АВ² - АВ²)/4) = √(3АВ²/4) = (АВ*√3) /2
S =1/2 * АС * СВ = 18√3 / 3
1/2 * ((АВ*√3)/2 * (АВ/2)) = 18√3 / 3
1/2 * ( (АВ²*√3) / 4 ) = 18√3 / 3
АВ²√3 / 8 = 18√3 / 3
3 *√3* АВ² = 18√3 * 8
АВ² = 144√3 / 3√3
АВ² = 48
АВ = √48 = √(16*3) = 4√3 - гипотенуза
СВ = 4√3 /2 = 2√3 - один катет
АС = (4√3 *√ 3)/2 = (4*(√3)²)/2 = 12/2 = 6 - второй катет, который лежит против угла В = 60°.
Ответ: АС = 6.