Предмет: Алгебра,
автор: BlayerHj
Пи интеграл от ^ 1 до -1 (1-x^2)dx
Приложения:
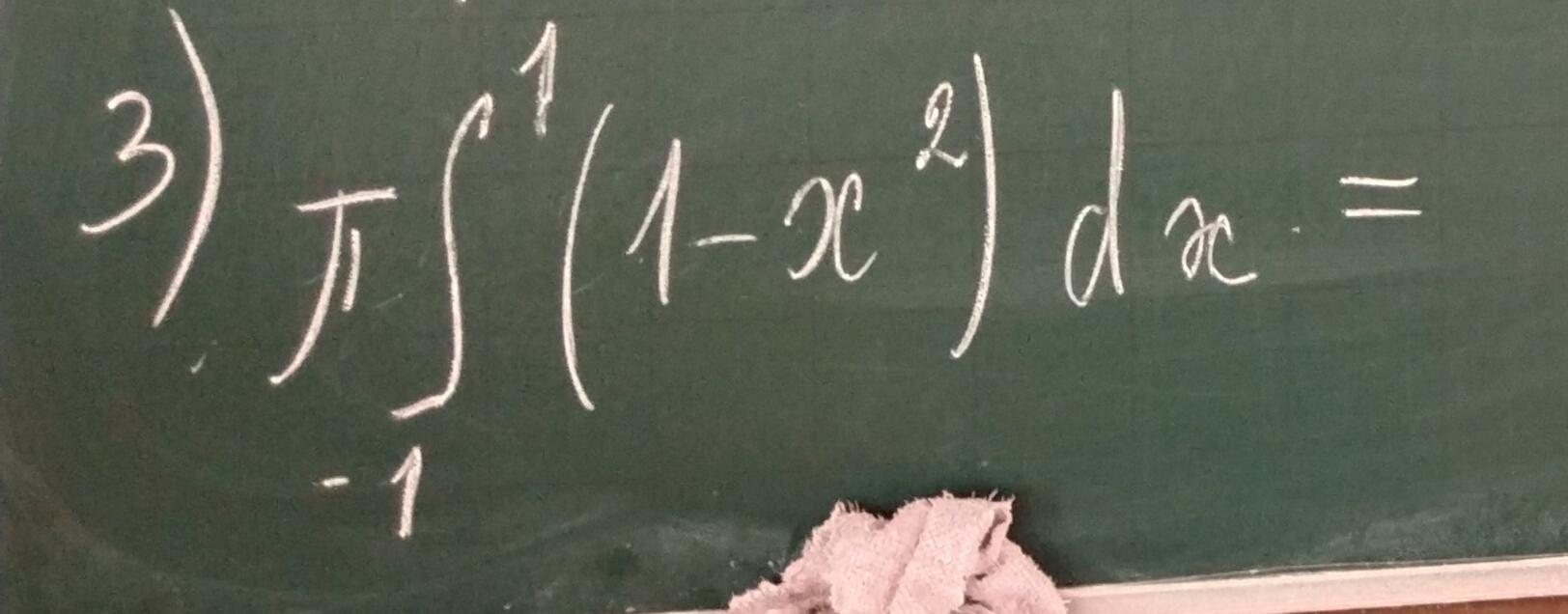
Ответы
Автор ответа:
1
Ответ:
Объяснение:
Вычислим сначала неопределенный интеграл:
. Так как константу можно вынести за интеграл, то
.
.
milana48588:
Помоги пожалуйста по алгебре 9 класс
Похожие вопросы
Предмет: Английский язык,
автор: werkut2
Предмет: Алгебра,
автор: Lev0607
Предмет: Қазақ тiлi,
автор: dandy2003
Предмет: Геометрия,
автор: alenadiamon
Предмет: Английский язык,
автор: Мехрибан11