Предмет: Алгебра,
автор: dianaladan948
СРОЧНО : ( х-1 )|х²+1| + |х-1| (х²+1) = 0
Приложения:
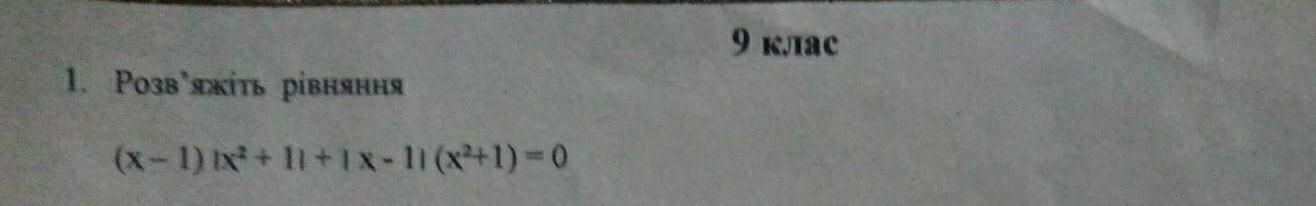
Simba2017:
так как x^2+1 больше 0, знак модуля можно убрать.
(x^2+1)(x-1+|x-1|)=0
x-1+|x-1|=0
a+|a|=0;|a|=-a-значит а 0 или отрицательно
тогда x-1 меньше или равно 0
значит х меньше или равно 1
Ответы
Автор ответа:
1
Ответ:
Объяснение:
х²+1 всегда больше нуля, значит просто опускаем модуль
Объединяем:
Ответ:
Автор ответа:
1
Ответ: хЄ (- ∞ ; 1 ] .
Объяснение:
( x - 1 )| x² + 1 | + | x - 1 |( x² + 1 ) = 0 ;
( x - 1 )( x² + 1 ) + | x - 1 |( x² + 1 ) = 0 ;
( x² + 1 )( x - 1 + | x - 1 | ) = 0 ;
x² + 1 ≠ 0 або x - 1 + | x - 1 | = 0 ;
розв"язуємо останнє рівняння :
| x - 1 | = - х + 1 ;
вираз під модулем дорівнює 0 при х = 1 .
1) х ≤ 1 , тоді - ( x - 1 ) = - ( x - 1 ) ; правильна рівність при хЄ (- ∞ ; 1 ] ;
2) x > 1 , тоді x - 1 = - х + 1 ; ----> 2x = 2 ; ----> x = 1 ∉ ( 1 ; + ∞ ) .
В - дь : хЄ (- ∞ ; 1 ] .
Похожие вопросы
Предмет: Математика,
автор: валерия364
Предмет: Математика,
автор: 161812
Предмет: Математика,
автор: Александр090
Предмет: Химия,
автор: nastymoroz4
Предмет: Математика,
автор: majtuffi