Предмет: Алгебра,
автор: Merifri
Помогите, плиизз. Хотя бы один)
Приложения:
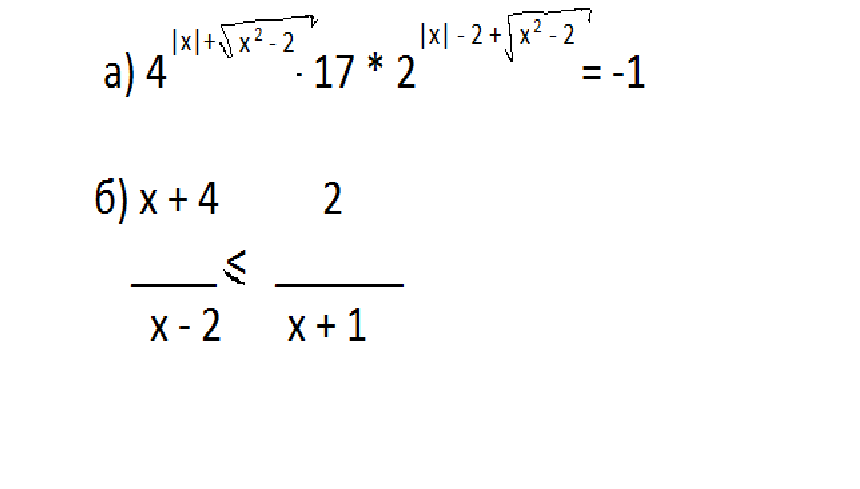
Ответы
Автор ответа:
0
Похожие вопросы
Предмет: Оʻzbek tili,
автор: makhzunadavidova707
Предмет: МХК,
автор: akatovapolina817
Предмет: Математика,
автор: bosdar
Предмет: Математика,
автор: mmmnnm