решите примеры буду благодарен
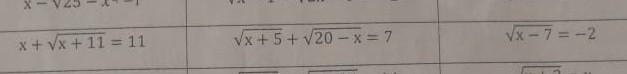
Ответы
Пошаговое объяснение:
1)
Через дискриминант
Так как
-беск<x
Тогда ответ
2)
Возведем обе части в квадрат
Опять возведем в квадрат
Через Виета
3) Также в квадрат возвести
1) x+sqrt(x+11)=11
11-x=sqrt(x+11)
121-22x+x^2=x+11
110-23x+x^2=0
D=529-440=89
x1=11,5+sqrt(89)/2
x1=11,5-sqrt(89)/2
Согласно ОДЗ 11-х больше либо равно 0.
Значит корень один:
Ответ:
х=11,5-0,5*sqrt(89)
2) sqrt(x+5)+ sqrt(20-х)=7
Пусть х=5у
sqrt(5)*(sqrt(y+1)+sqrt(4-y))=7
y+1+4-y+2*sqrt(y+1)*sqrt(4-y)=49/5
2*sqrt(y+1)*sqrt(4-y)=49/5-5
sqrt(y+1)*sqrt(4-y)=4,9-2,5
(y+1)(4-y)=2,4
-y^2+4+3y=2,4
y^2-3y-1,6=0
D=9+6,4=15,4
y1=1,5+sqrt(15,4)/2
y2=1,5-sqrt(15,4)/2
Проверкой убеждаемся, что оба корня подходят по ОДЗ.
Ответ:
х1=7,5+2,5*sqrt(15,4)
х2=7,5-2,5*sqrt(15,4)
3)
sqrt(x-7)=-2
Ответ: вещественных решений нет (правая часть отрицательна)