100 БАЛЛОВ!
В треугольнике АВС известно, что
угол А = 40°, угол В = 20°, АВ - ВС = 4 см. Найдите биссектрису треугольника, проведённую из угла С
Ответы
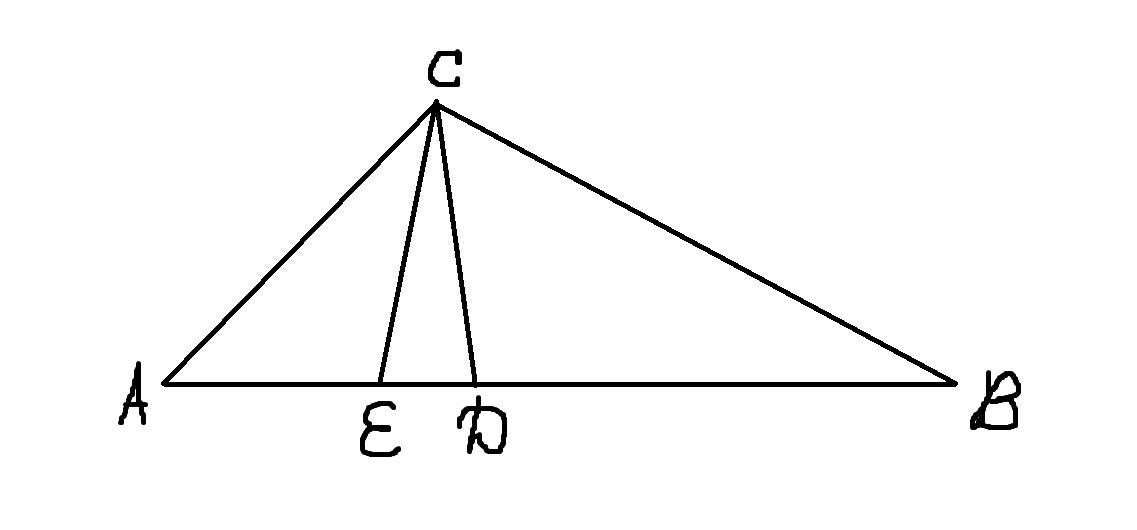
CD - биссектриса угла C
Дополним построение:
Добавим точку E, лежащую на AB
Получается EB = BC , т.е. Δ ECB является равнобедренным.
Угол ∠ B = 20°
Значит ∠ ECB = ∠CEB = ( 180° - 20° ) / 2 = 80°
В Δ ACB углы ∠A и ∠B известны, значит:
∠C = 180° - 20° - 40° = 120°
Половина ∠ C = ∠ ACD = ∠ BCD = 120° / 2 = 60°
В Δ ACD = ∠ A и ∠ ACD известны, значит:
∠ ADC = 180° - 40° - 60° = 80°
Рассмотрим треугольник Δ ECD
Углы ∠ CED ( = ∠ CEB ) и ∠ CDE ( = ∠ ADC ) равны, значит Δ является равнобедренным
EC = CD ∠ ECD = 180° - 80° - 80° = 20°
Рассмотрим треугольник Δ ACE
Угол ∠ A известен, угол ∠ACE можно получить как разницу углов ∠ACD и ∠ECD
∠ ACE = 60° – 20° = 40°
∠ ACE = ∠ A, то есть Δ ACE также равнобедренный
AE = EC
Осталось найти биссектрису CD
CD = EC = AE = AB - EB = AB - BC = 4
Ответ: 4