Предмет: Алгебра,
автор: elena200403
439??
Не подскажите, как решить?
Приложения:
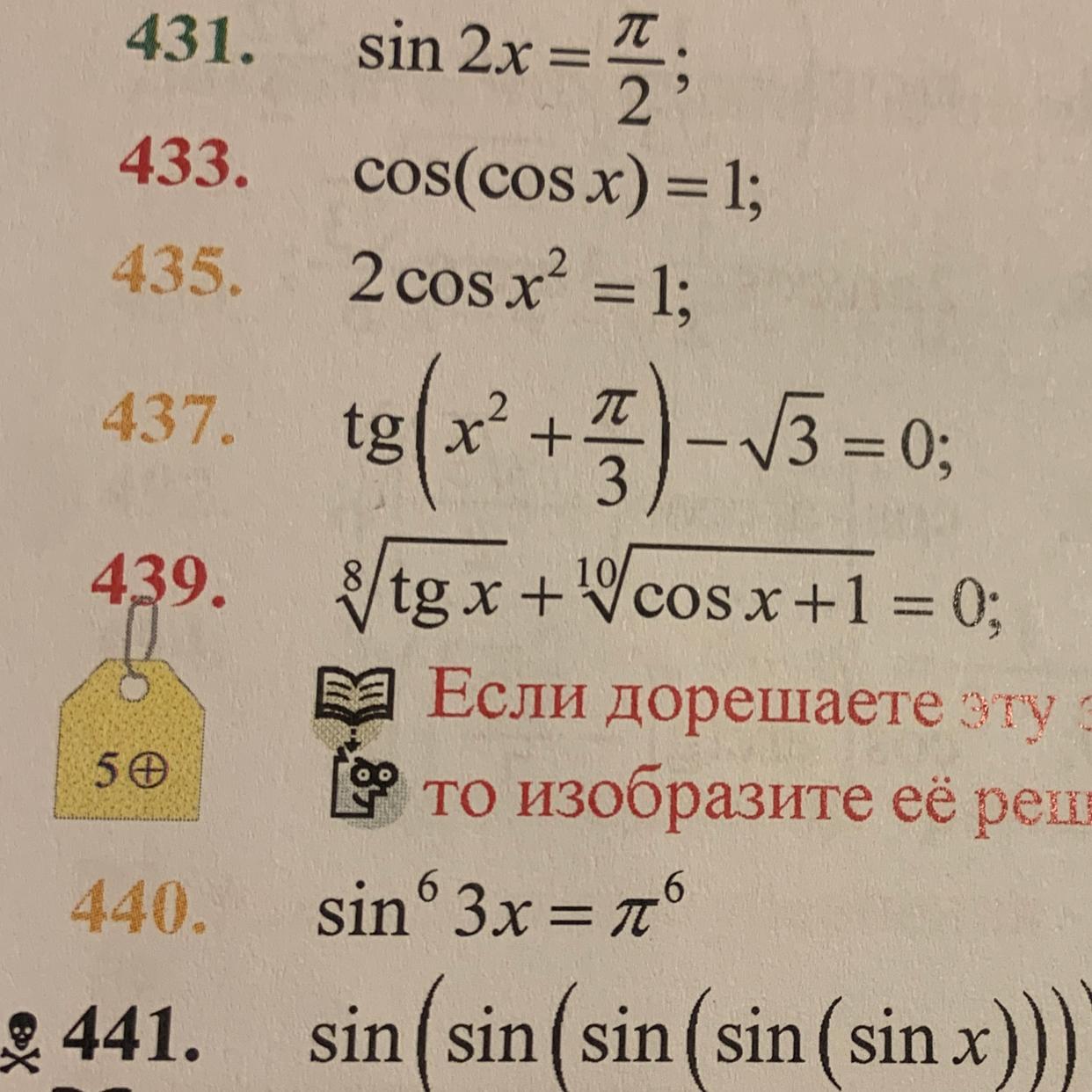
Ответы
Автор ответа:
2
Ответ:
⁸√tg(x)+¹⁰√(cos(x)+1)=0
Выражение под корнем должно быть положительным
{ tg(x)>0
{ cos(x)+1>0 cos(x)>-1 x∈ℝ
cos ( косинус ) всегда больше -1 потому что область значения косинуса равна [ -1 1 ]
Остаётся только
tg(x)>0 x∈[ πk , π/2+πk ) k∈ℤ
Решаем уравнение
⁸√tg(x)= -¹⁰√(cos(x)+1)
Правая часть уравнения всегда отрицательна
А левая всегда положительна
Из этого выходит что этр равенство выполняется только и только когда две части равенство равны нулю
{ ⁸√tg(x)=0 { tg(x)=0 { x=πn , n∈ℤ
{ ¹⁰√(cos(x)+1)=0 { cos(x)= -1 { x=π+2πp , p∈ℤ
Общий ответ системы это
x = π+2πp , p∈ℤ
Ответ : x = π+2πp , p∈ℤ
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Математика,
автор: kk111
Предмет: Окружающий мир,
автор: 7zvon77
Предмет: Литература,
автор: nabievamarina26
Предмет: Геометрия,
автор: Nanajeon1997