Предмет: Алгебра,
автор: hacikirikivauvausens
Решить геометрию надо
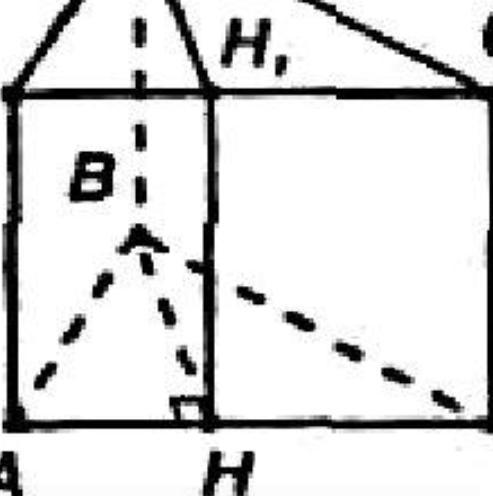
1) В прямой треугольнике призме стороны основания равны 10,17, 21, а высота призмы 18 см. Найдите площадь сечения проведённого через боковое ребро и меньшую высоту основания
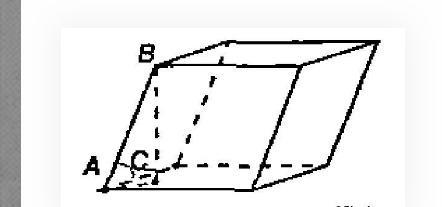
2) боковое ребро наклонной призмы равно 15 см и наклонено к плоскости основания под углом 30 градусов. Найдите высоту призмы
Ответы
Автор ответа:
0
Ответ: 1)144см²; 2)7,5см
Объяснение:
1) Данным сечением является прямоугольник BHH1B1 со сторонами ВВ1=18 см и ВН; где ВН — меньшая высота ΔАВС. Далее, площадь основания с одной стороны равнa:
S=√p(p-a)(p-b)(p-c)=√24(24-10)(24-17)(24-21)=84(см²)
С другой стороны
S=½ AC*BH
так что
BH=2S/AC=2*84/21=8(см²)
Тогда искомая площадь сечения равна
S1=BB1*BH=18*8=144(см²)
2). ВО — перпендикуляр к основанию, так что ΔАВО — прямоугольный. Значит, BC=ABsin∠BAC=15sin30° =7,5 (см).
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: amirjaber97
Предмет: Математика,
автор: Монри
Предмет: Русский язык,
автор: kkrist
Предмет: Биология,
автор: 744305
Предмет: Математика,
автор: Ооллог