Предмет: Алгебра,
автор: Аноним
Найти область сходимости степенного ряда.
Приложения:
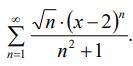
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: вик109
Предмет: Математика,
автор: R438129576m
Предмет: Математика,
автор: анюта390
Предмет: Алгебра,
автор: patis123
Предмет: Биология,
автор: Squze
https://znanija.com/task/45946303