Предмет: Геометрия,
автор: shaimerdenovadil9G
Помогите сделать Геометрию
Приложения:
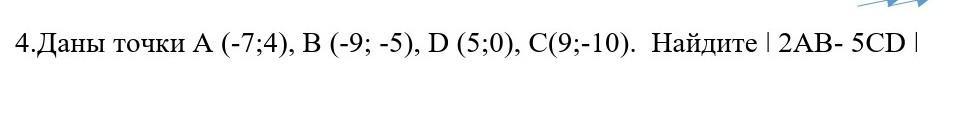
Ответы
Автор ответа:
1
Возможны два решения.
Если в условии нужно найти модуль разности длин отрезков:
Ответ: 10√29 - 2√85.
==========================================
Если в условии нужно найти длину разности векторов:
Ответ: 4√305.
Похожие вопросы
Предмет: Математика,
автор: Чупакабра1111
Предмет: Русский язык,
автор: nata8810
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: Yanna04Filll
Предмет: Математика,
автор: Ekaterina2343