Предмет: Алгебра,
автор: eyastrebkov111
Подайте у вигляді многочлена чи роціонального дробу, завданя Г и Б.
Приложения:
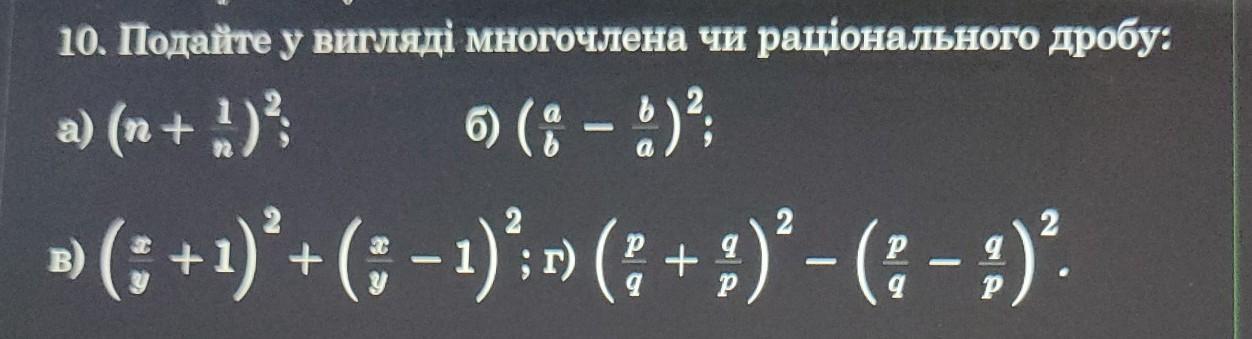
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Химия,
автор: siriusoriginal
Предмет: Химия,
автор: kirilltrusov1
Предмет: Русский язык,
автор: алишкк
Предмет: Математика,
автор: halfling
Предмет: Геометрия,
автор: vasyan20039