Предмет: Алгебра,
автор: dfoeubdn
найдите функцию, обратную для функции y=-x²+6x-10, D(y)=[3;+∞)
Ответы
Автор ответа:
1
Ответ:
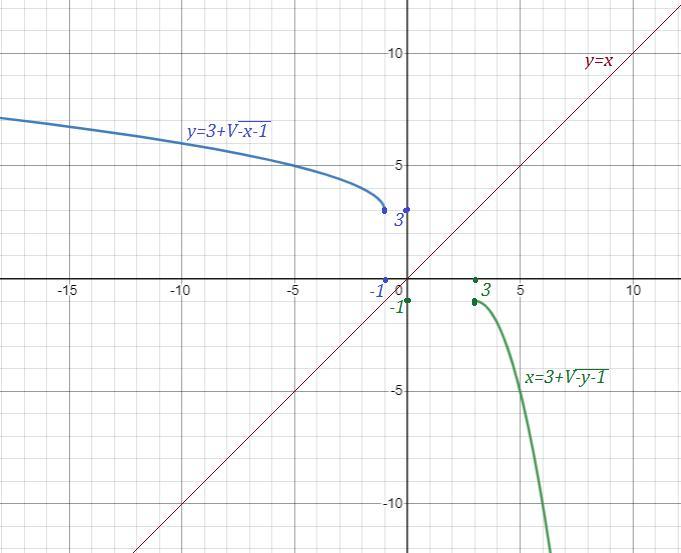
Графики взаимно обратных функций симметричны относительно биссектрисы 1 и 3 координатных углов (у=х) .
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: Милена55866
Предмет: Английский язык,
автор: Filatova197470
Предмет: Математика,
автор: Tyson12
Предмет: Математика,
автор: Внешний
Предмет: Русский язык,
автор: sanyaCher