Предмет: Геометрия,
автор: nranneva2017
Очеееень срооочнооо!!!!
Найдите объём правильного четырехугольника пирамиды, сторона основания которой равна 6, а боковое ребро равно

Ответы
Автор ответа:
1
Ответ:
48ед³
Объяснение:
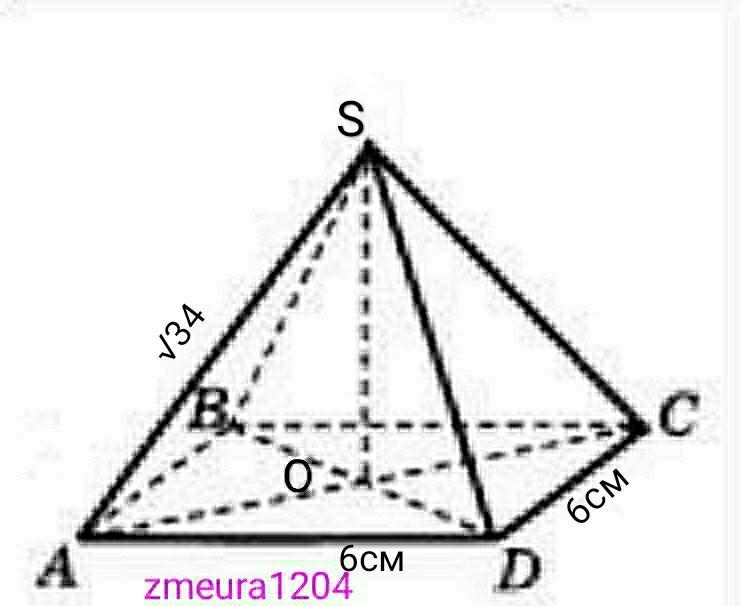
Дано:
SABCD- пирамида.
ABCD- квадрат
АВ=6ед
SA=SB=SC=SD=√34 ед
V=?
Решение.
АС=АВ√2=6√2ед диагональ квадрата
АО=АС/2=6√2/2=3√2 ед.
Теорема Пифагора
SO=√(SA²-AO²)=√((√34)²-(3√2)²)=
=√(34-18)=√16=4ед.
Sосн=АВ²=6²=36ед²
V=1/3*Sосн*SO=1/3*36*4=48ед³
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: sashakiselev0
Предмет: Русский язык,
автор: lololoshka333227
Предмет: Русский язык,
автор: Enderkotia228
Предмет: Математика,
автор: Филин7777
Предмет: Литература,
автор: Anutik555555