Предмет: Алгебра,
автор: kalamkaszumagul
Найдите производную функции
Приложения:
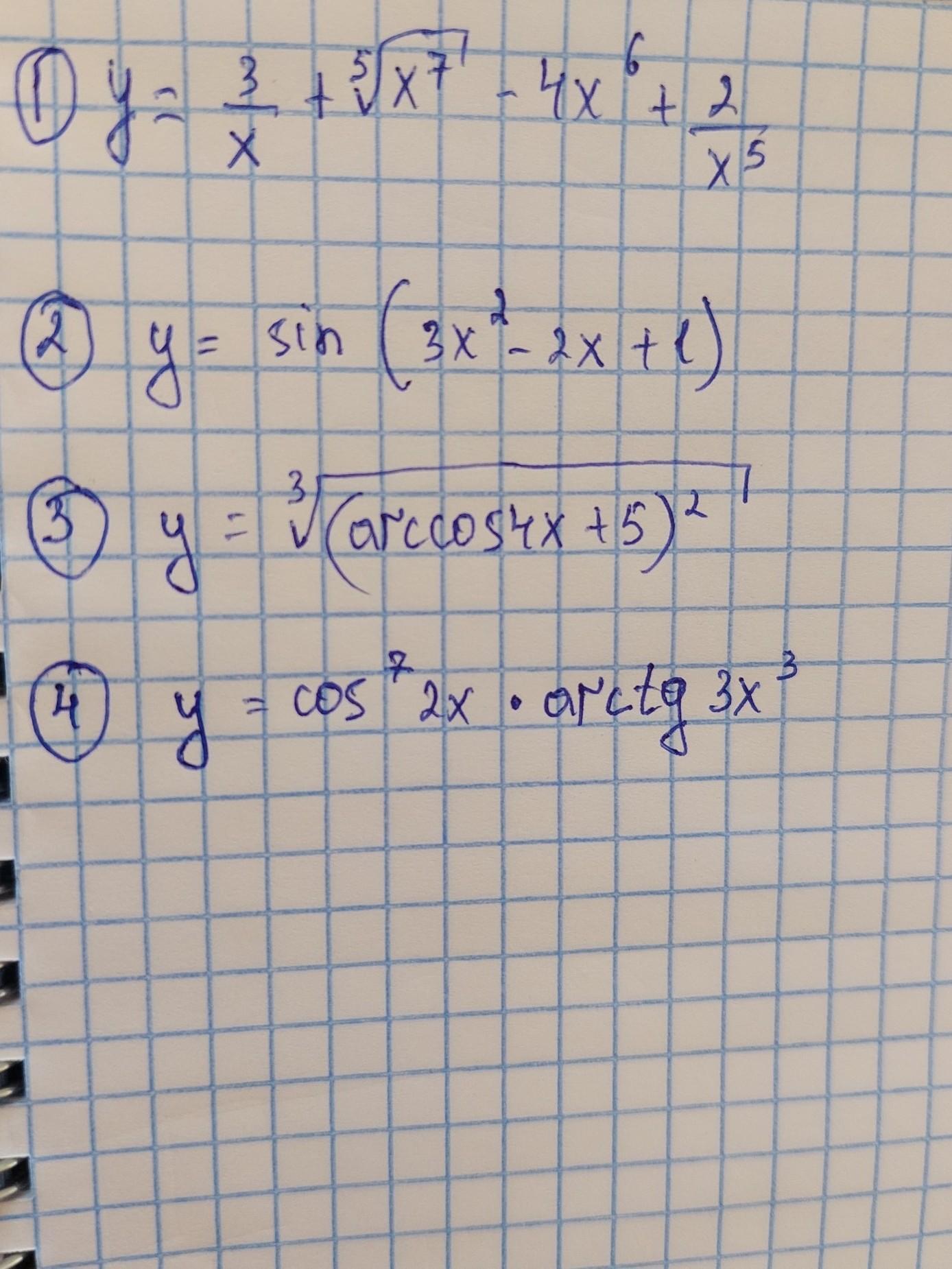
Ответы
Автор ответа:
0
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: ученик744
Предмет: Русский язык,
автор: karishkaMey
Предмет: Русский язык,
автор: ruxa4
Предмет: Английский язык,
автор: bb1