Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста!
Найти общее решение дифференциального уравнения.
Приложения:
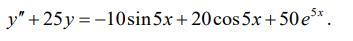
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: bloovvfx
Предмет: Українська мова,
автор: Alltna26073
Предмет: Русский язык,
автор: дюхаточкару1
Предмет: Физика,
автор: Чебурек1234
Предмет: Геометрия,
автор: un670001