Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста!
Исследовать непрерывность функции f (x). Найти точки разрыва функции и определить их характер. Выполнить геометрическую иллюстрацию
Приложения:
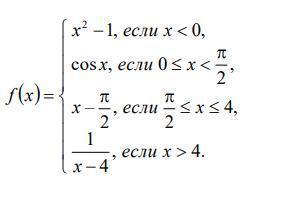
Ответы
Автор ответа:
1
Ответ:
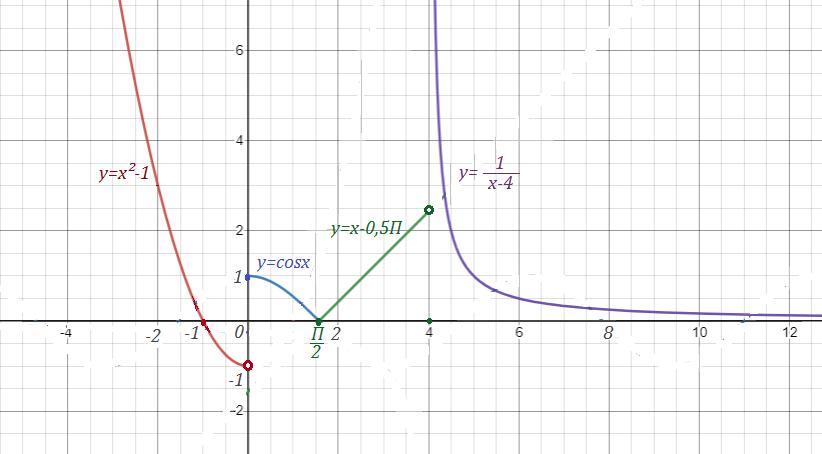
х=0 - точка разрыва 1 рода (скачок = 2) .
При х=П/2 функция непрерывна .
При х=4 функция терпит разрыв 2 рода .
Приложения:
Похожие вопросы
Предмет: Математика,
автор: black185
Предмет: Английский язык,
автор: девчёнка123
Предмет: Русский язык,
автор: юленька42
Предмет: Математика,
автор: dashasolodilova
Предмет: Информатика,
автор: Eeslami