З розвязками, даю 50 балів!
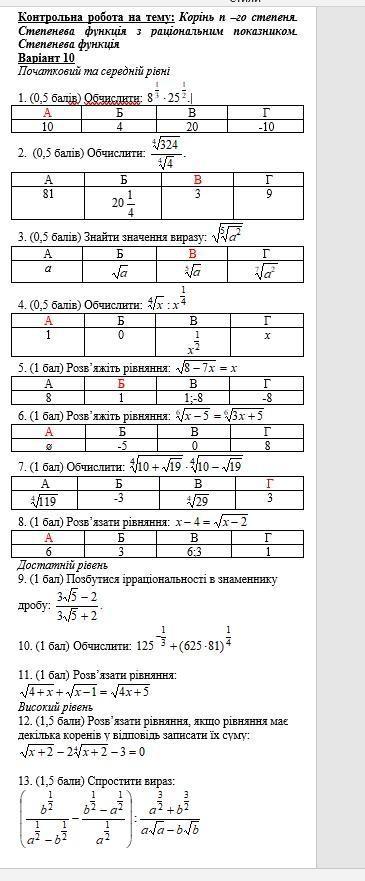
Ответы
Ответ:
Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением. Например:
\begin { align } \cos(nx) & = \mathrm { Re } \ { \ e^ { inx } \ \ } = \mathrm { Re } \ { \ e^ { i(n-1)x } \cdot e^ { ix } \ \ } \\ & = \mathrm { Re } \ { \ e^ { i(n-1)x } \cdot (e^ { ix } + e^ { -ix } - e^ { -ix } )\ \ } \\ & = \mathrm { Re } \ { \ e^ { i(n-1)x } \cdot \underbrace { (e^ { ix } + e^ { -ix } ) } _ { 2\cos(x) } - e^ { i(n-2)x } \ \ } \\ & = \cos[(n-1)x]\cdot 2 \cos(x) - \cos[(n-2)x]. \end { align }
Данная формула используется для рекурсивного вычисления значений cos(nx) для целых значений n и произвольных значений x (в радианах).
(6A + 4B)cos3x + (4A - 6B)sin3x + x((-5A)sin3x + (12A - 5B)cos3x) + (25A*sin3x + 25B*cosX) = sinx