Предмет: Геометрия,
автор: Yura2626
СРОЧНО СРОЧНО СРОЧНО
Приложения:

Ответы
Автор ответа:
1
Дано:
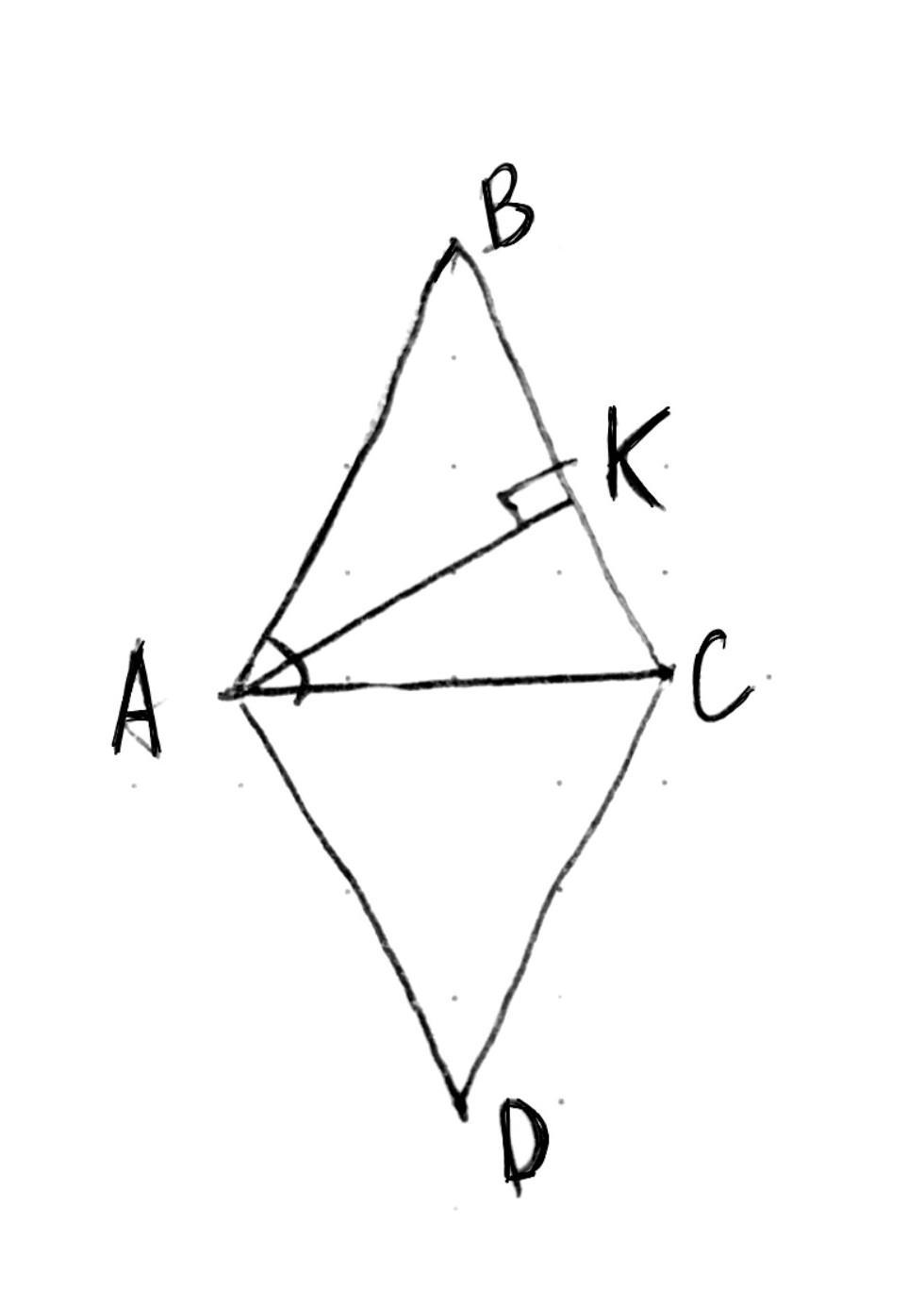
ромб ABCD
= 20см
∠BAC = 75°
Найти: высоту AK
Решение:
У ромба все стороны равны,
= 4a, где a — сторона ромба,
4a = 20см, a = 20см ÷ 4 = 5см,
AB = BC = CD = AD = 5см.
Диагонали ромба являются биссектрисами его углов =>
∠BAC = ∠CAD = 1/2 ∠BAD,
∠BAD = 2 ∠BAC = 2 × 75° = 150°.
Соседние углы ромба в сумме равны 180° =>
∠BAD + ∠ABC = 180°,
∠ABC = 180° – ∠BAD = 180° – 150° = 30°.
Рассмотрим треугольник ABK.
AK — высота => ∠ABK = 90° => треугольник ABK — прямоугольный.
∠ABK = ∠ABC = 30°.
В прямоугольном треугольнике катет, лежащий против угла в 30°, равен половине гипотенузы => AK = 1/2 AB = 1/2 × 5см = 2.5см
Ответ: 2.5см
Приложения:
Yura2626:
кинул вопрос хочешь посмотри
Похожие вопросы
Предмет: Обществознание,
автор: dianabobkova714
Предмет: Английский язык,
автор: zhansultannaur
Предмет: Другие предметы,
автор: Моллі
Предмет: Русский язык,
автор: BlueBird666
Предмет: Математика,
автор: 1Сара1