Предмет: Математика,
автор: pyatachorg
Помогите пожалуйста срочно
1) избавиться от иррационального знаменателя
2) Упростить выражение
Приложения:
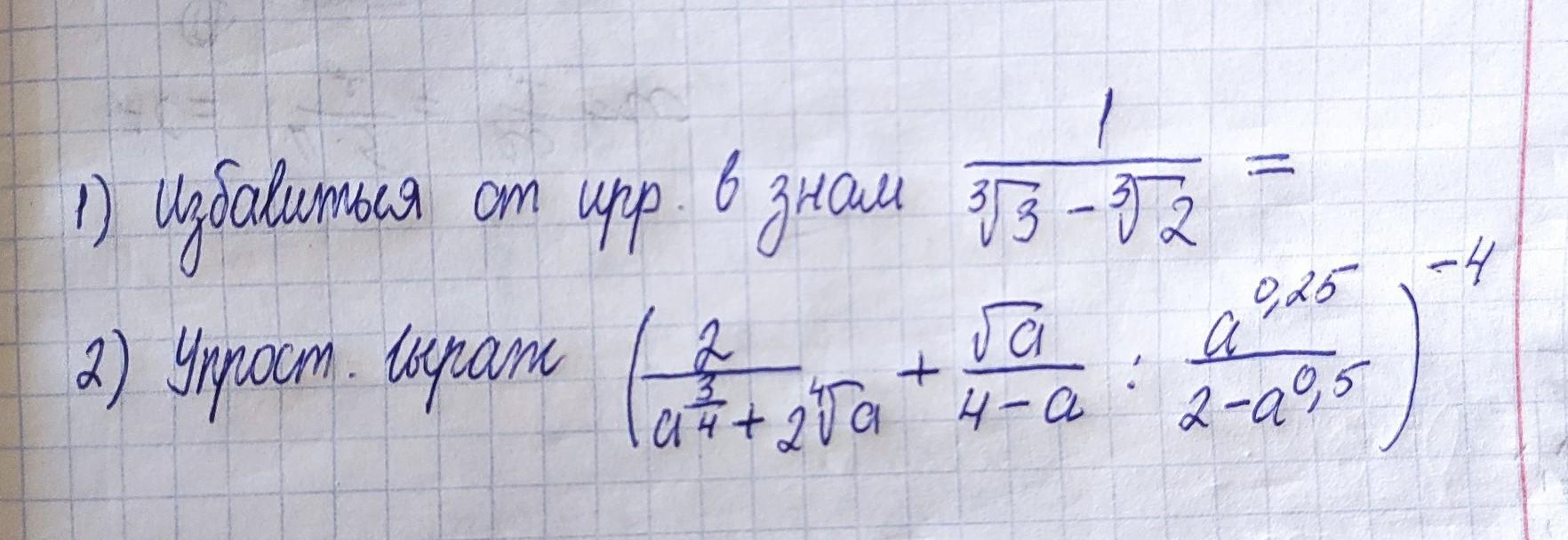
Ответы
Автор ответа:
0
Ответ:
pyatachorg:
здравствуйте ! можете пожалуйста помочь с заданием , вопрос в профиле
Похожие вопросы
Предмет: Английский язык,
автор: FlashGirl
Предмет: Русский язык,
автор: OleG023009
Предмет: Музыка,
автор: пуп777
Предмет: Химия,
автор: Stroganov1
Предмет: Литература,
автор: Yuliya110507