Предмет: Геометрия,
автор: aitbaisha2708
Стороны треугольника: в соотношении 3: 4: 5, его периметр 60 см. Найдите стороны треугольника, вершины которого являются серединами сторон этого треугольника.
Ответы
Автор ответа:
2
Дано:
AB : BC : AC = 3 : 4 : 5
PΔABC = 60см
Найти: стороны ΔABC.
Решение:
т.к. PΔABC = 60см =>
=> 3x+4x+5x=60см
12x = 60см
x = 5см
AB = 3x = 3 * 5 см = 15см
BC = 4x = 4 * 5 см = 20см
AC = 5x = 5 * 5 см = 25см
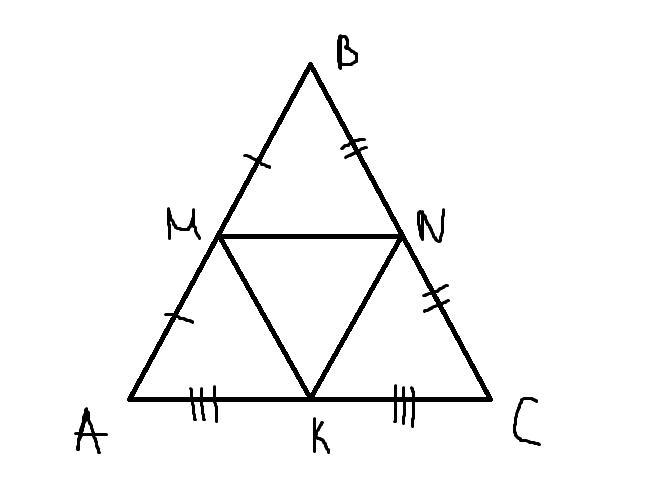
Точки M,N,K - середины сторон ΔABC.
MN - средняя линия ΔABC =>
=> MN = = 12,5см
MK = = 10см
NK = = 7,5см
Ответ: 12,5см; 10см; 7,5см
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Vika16261
Предмет: Математика,
автор: nadegda12x
Предмет: Математика,
автор: 11Диана112
Предмет: Математика,
автор: tipaanya
Предмет: Қазақ тiлi,
автор: Викушечка0