Предмет: Алгебра,
автор: Аноним
Помогите, пожалуйста, срочно!
Исследовать функцию z = z (x, y) на экстремум.
Приложения:
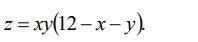
Ответы
Автор ответа:
1
Ответ:
В точке функция
имеет максимум
Объяснение:
Пусть x = 0
y(12 - y) =2xy
y(12 - y) =2y * 0
y(12 - y) = 0
(0;0) , (0;12)
Пусть y = 0
x(12 - x) =2xy
x(12 - x) =2x * 0
x(12 - x) = 0
(0;0) , (12;0)
(4;4)
Точки подозрительные на экстремум:
Так как то в точке
экстремума не существует
Так как то в точке
экстремума не существует
Так как и
то в точке
максимум функции
Так как то в точке
экстремума не существует
Пример еще в процессе решения
О вот теперь полное решение
Спасибо огромное!
А можете помочь с вопросом еще? ссылка выше была, пожалуйста
А можете помочь с вопросом еще? ссылка выше была, пожалуйста
Нет, я диффурами помочь не смогу . Напиши https://znanija.com/app/profile/8173857/answers
А с рядами?
Похожие вопросы
Предмет: Английский язык,
автор: OlgaGarkava
Предмет: Математика,
автор: настя3126
Предмет: Русский язык,
автор: nata060905
Предмет: Алгебра,
автор: elvira661
Предмет: Биология,
автор: Alya031333
можешь тут помочь, пожалуйста!
https://znanija.com/task/45858760