Предмет: Геометрия,
автор: elinakramer666
пожалуйста срочно надо помогите с дано найти решением и рисунком
Приложения:

Ответы
Автор ответа:
1
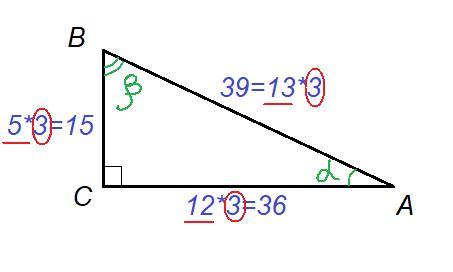
Дано: ΔABC; AB = 39; cos α = 12/13; cos β = 5/13
Найти: SΔ
Решение:
Числа 5, 12 и 13 - это Пифагорова тройка:
То есть для треугольника со сторонами, кратными числам 5, 12 и 13, выполняется теорема Пифагора, значит, заданный треугольник прямоугольный, причём гипотенуза равна 39, так как к ней прилегают острые углы.
В прямоугольном треугольнике косинус острого угла равен отношению прилежащего катета к гипотенузе. Приведём косинусы к знаменателю 39:
Так как гипотенуза равна 39, то катеты равны 36 и 15.
Площадь прямоугольного треугольника равна полупроизведению катетов:
Ответ: 270.
Приложения:
Похожие вопросы
Предмет: Окружающий мир,
автор: 1231538
Предмет: Химия,
автор: davidara
Предмет: Математика,
автор: УБеллочка
Предмет: Алгебра,
автор: majorova20121
Предмет: Русский язык,
автор: lvovaels