Question

Решите плиз есть скрин для удобства
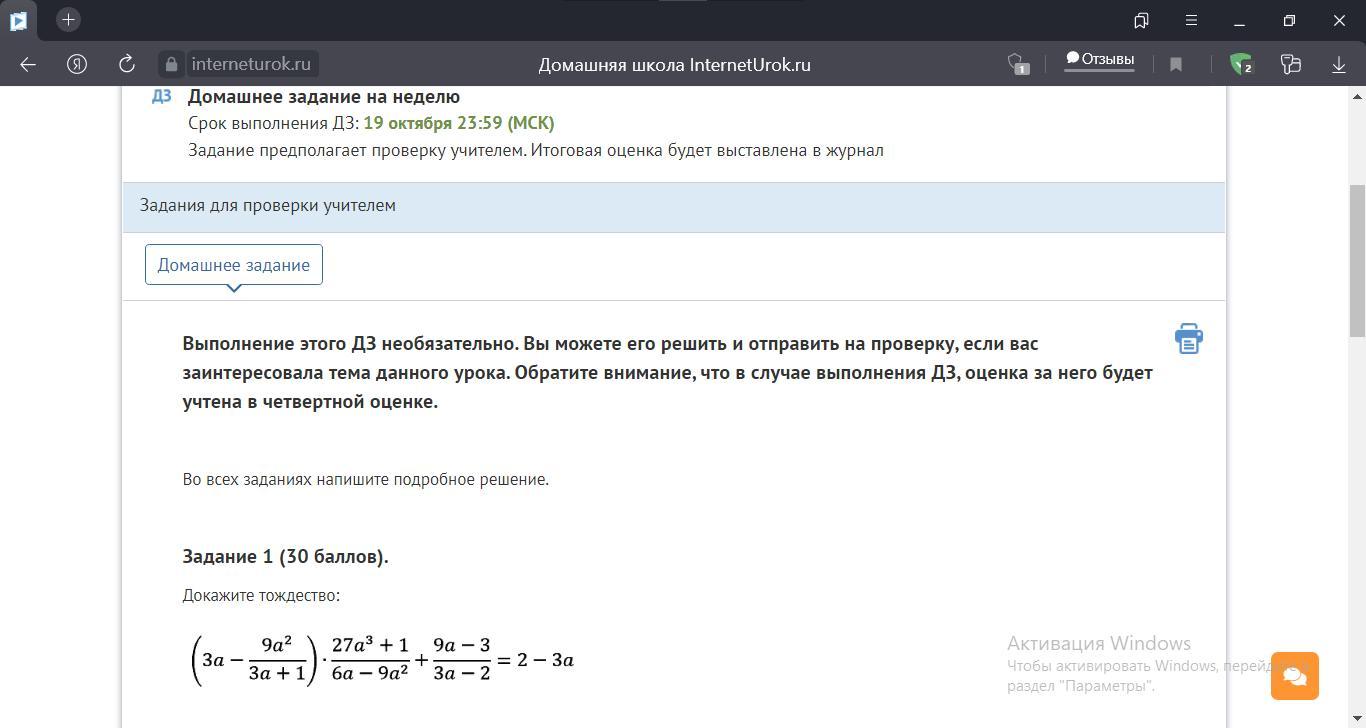
Задание 1 (30 баллов).

Докажите тождество:

(3a-9a^2/3a+1)*27a^3+1/6a-9a^2+9a-3/3a-2=2-3a

^ -степень

* -умножение

/ -дробь или деление

Answer 1

Ответ:

Тождество верно

Объяснение:

$(3a - \frac{9a^2}{3a+1} )\frac{27a^3 +1}{6a-9a^2} + \frac{9a-3}{3a-2} =2-3a\\(\frac{3a(3a+1) -9a^2}{3a+1} )\frac{27a^3 +1}{3a(2-3a)} - \frac{9a-3}{2-3a} =2-3a\\(\frac{3a(3a+1) -9a^2}{3a+1} )\frac{27a^3 +1}{3a(2-3a)} =2-3a+\frac{9a-3}{2-3a}\\(\frac{3a(3a+1) -9a^2}{3a+1} )\frac{27a^3 +1}{3a(2-3a)} =\frac{(2-3a)^2 +9a-3}{2-3a}\\(\frac{3a(3a+1) -9a^2}{3a+1} )\frac{27a^3 +1}{3a} =(2-3a)^2 +9a-3\\(\frac{9a^2+3a -9a^2}{3a+1} )\frac{27a^3 +1}{3a} = (2-3a)^2 +9a-3$

$(\frac{9a^2+3a -9a^2}{3a+1} )\frac{27a^3 +1}{3a} =(2-3a)^2 +9a-3\\(\frac{3a}{3a+1} )\frac{(3a)^3 +1}{3a} =(2-3a)^2 +9a-3\\\frac{(3a)^3 +1 }{3a+1} =(2-3a)^2 +9a-3\\(3a)^3 +1 =((2-3a)^2 +9a-3)(3a+1)\\27a^3 +1 =(4-12a + 9a^2 +9a-3)(3a+1)\\27a^3 +1 =(1-3a + 9a^2)(3a+1)\\27a^3 +1 =3a-9a^2 + 27a^3+1-3a + 9a^2\\0 =-9a^2 + 9a^2\\0 =0$

Тождество верно

Answer 2

Решение задания прилагаю