Предмет: Алгебра,
автор: zhansaya200405
Вычислите площадь фигуры ограниченной линиями: y=x^2-4x+4 и y=0 х=0
Ответы
Автор ответа:
0
Ответ:
Объяснение:
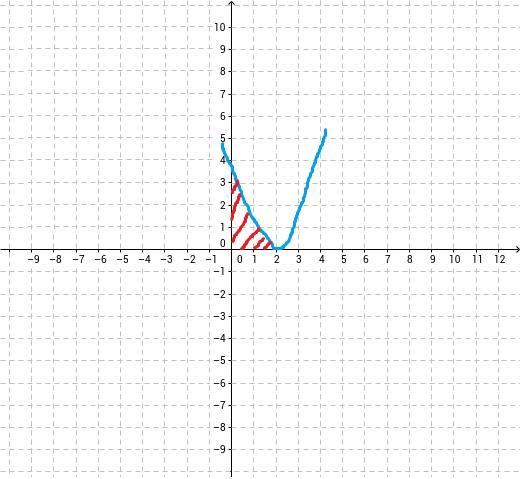
График на рисунке.
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: salavat9898
Предмет: Русский язык,
автор: ackles18
Предмет: Русский язык,
автор: лени2
Предмет: Алгебра,
автор: pRoToTyPe95wF
Предмет: Математика,
автор: svetaaa77