Предмет: Геометрия,
автор: hi386891
Найдите вектор x из условия PB-OD+x+MC=PA-BM-OA Срочно С ОБЪЯСНЕНИЕМ, ПОМОГИ ПЛИЗ, МОДЕРАТОРЫ, Я ВАС ПРОШУ, СРОЧНО
Ответы
Автор ответа:
3
Для решения уравнения с векторами воспользуемся обычными правилами решения линейных уравнений. Неизвестный вектор оставляем слева, все остальные переносим вправо, при этом меняя знак на противоположный:
Если вектор задан двумя точками, то противоположный вектор задан теми же точками, но в обратном порядке:
Правило треугольника сложения векторов:
Переместительный закон сложения векторов:
=========================================
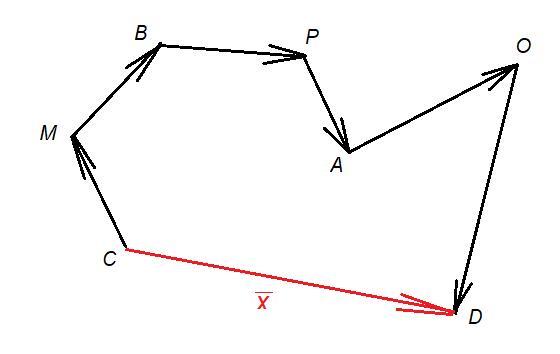
Каждая точка M,B,P,A,O является концом одного вектора и началом следующего, поэтому при сложении работает правило многоугольника (похожее на правило треугольника).
Приложения:
Похожие вопросы
Предмет: Математика,
автор: Олик2403
Предмет: Математика,
автор: lsobyaninaЛиза
Предмет: Английский язык,
автор: linkek
Предмет: Русский язык,
автор: 11111111111й11111111
Предмет: Геометрия,
автор: Nastya18141