Предмет: Алгебра,
автор: Jsh158
100 БАЛЛОВ ОТДАМ!
Уважаемые NNNLLL54!
Мне помогите пожалуйста!
100 баллов отдам!
Там надо сравнить.Мне надо с решением!
Приложения:

Ответы
Автор ответа:
0
Надеюсь правильно....
Приложения:
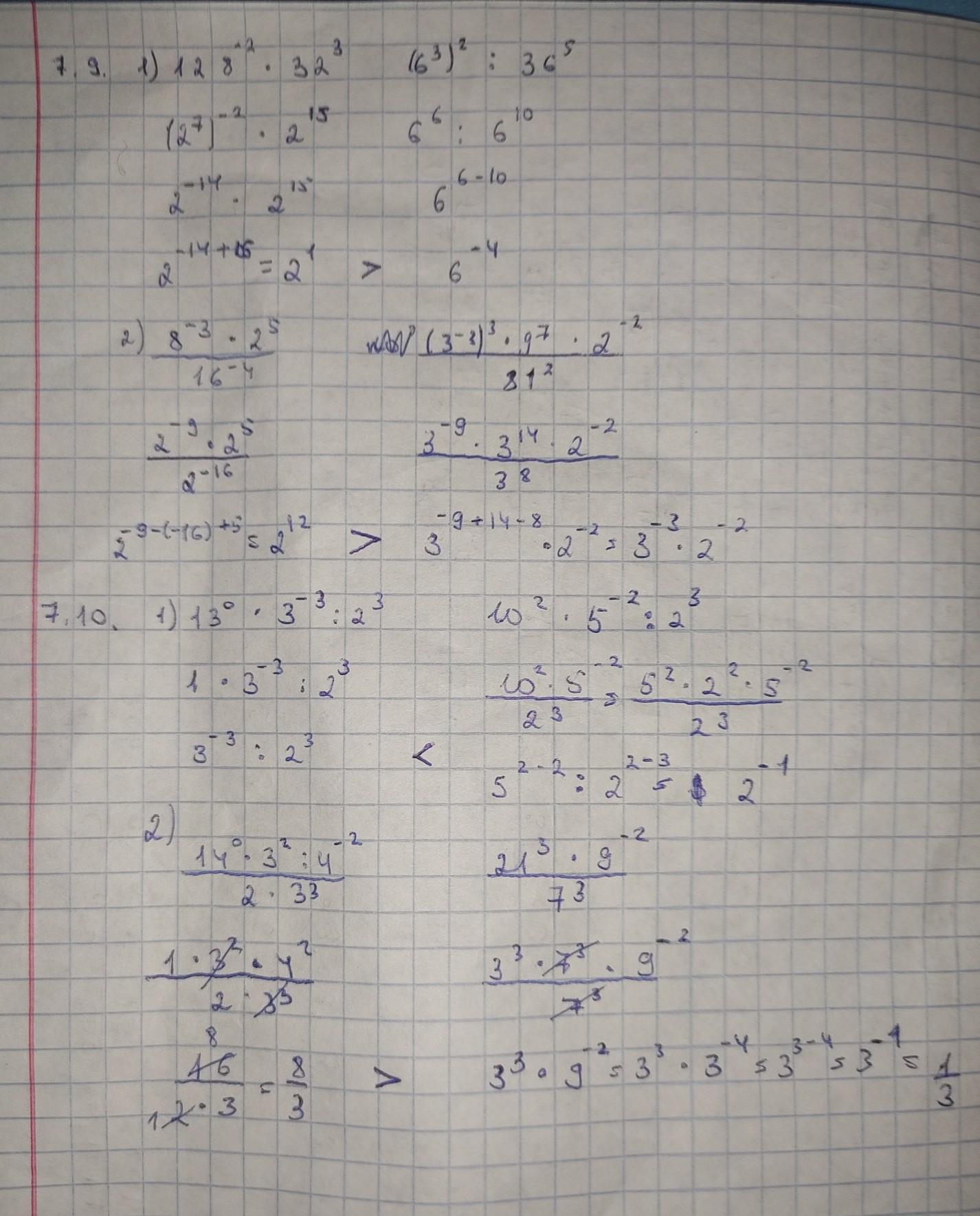
Автор ответа:
1
Ответ:
Если дроби имеют одинаковый числитель, то меньше та дробь, знаменатель которой больше .
Похожие вопросы
Предмет: Физика,
автор: nekrasovaalevt
Предмет: Математика,
автор: dashasorokina567796
Предмет: Алгебра,
автор: Marusiait99
Предмет: География,
автор: глеб413