Предмет: Алгебра,
автор: Akakakl
Нужно решить систему иррационального уравнения
(прошу если не знаете не писать в ответ чтото)
Приложения:
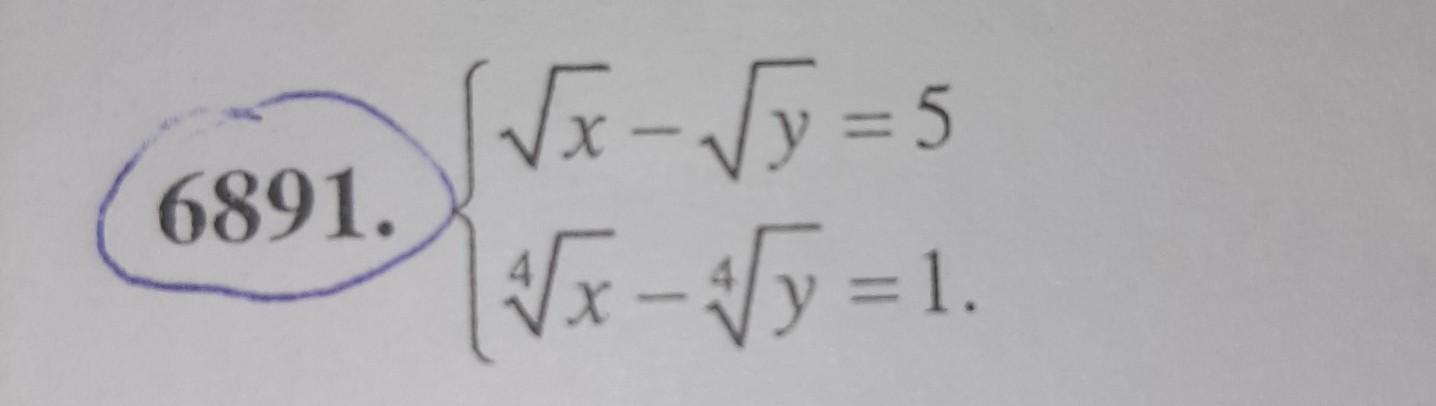
sfahsnova101:
можешь пожалуйста мне помочь последний и пред последний задание в моём профиле
посмотрю
спасибо большое
Ответы
Автор ответа:
1
ОДЗ:
Ответ:
Похожие вопросы
Предмет: Алгебра,
автор: Superme
Предмет: Математика,
автор: Элен20
Предмет: Русский язык,
автор: MrMARKOR
Предмет: Экономика,
автор: Babena