Предмет: Алгебра,
автор: assasin6998
пж хелп 100 баллов )
Приложения:
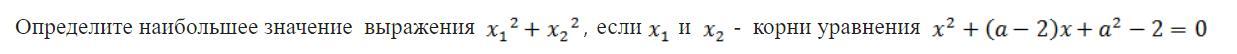
tamarabernukho:
12
А как ты решил?
Воспользуйтесь т.Виета
(x1)^2+(x2)^2=(x1+x2)^2-2x1*x2
=(2-a)^2-2(a^2-2)=-a^2-4a+8
Парабола, ветви вниз, наиб.значение в вешине параболы
С телефона оформлять не буду..
cпс
Ответы
Автор ответа:
1
Ответ:
12
Объяснение
Вот приложил решение твоей задачи
Приложения:

Автор ответа:
1
Ответ  12
12
Объяснение:
Максимальное значение достигается при вершине параболы
- Формула для нахождения координат вершины параболы :
Похожие вопросы
Предмет: Биология,
автор: Zulfira98
Предмет: Алгебра,
автор: gulmem
Предмет: Окружающий мир,
автор: Nastusha2017
Предмет: Литература,
автор: ScripTys