Предмет: Алгебра,
автор: frogg0
ВЫЧИСЛИТЕ ПРОИЗВОДНУЮ
Приложения:
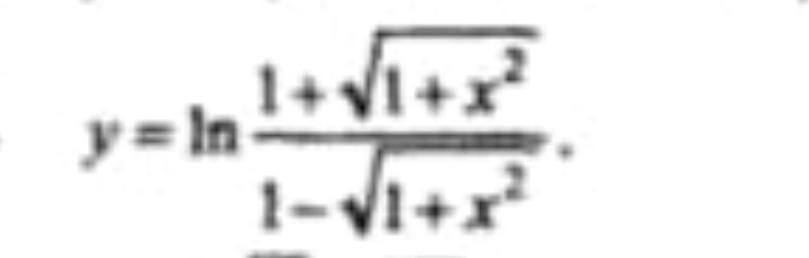
Ответы
Автор ответа:
1
Объяснение:
Пусть
Ответ:
Похожие вопросы
Предмет: Английский язык,
автор: lens5
Предмет: Алгебра,
автор: nastia2001tttt
Предмет: Геометрия,
автор: Edya6201
Предмет: Химия,
автор: Ixvjvcg
Предмет: Математика,
автор: dimost187