Предмет: Алгебра,
автор: Miа16
Алгебра. Даю 10 баллов. Решить 5-8. С подробным объяснением.
Приложения:
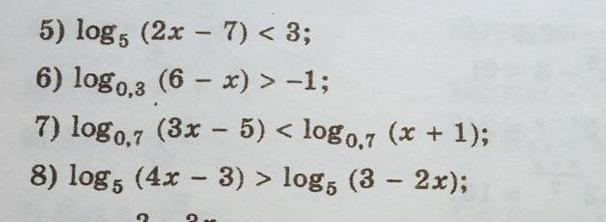
Ответы
Автор ответа:
1
Miа16:
Почему в 7 примере поменяли знак?
и в 8 так же
Если основание логарифма больше единицы, то знак не меняется, а если 0
поняла, спасибо)
почему- то половина комментария не отразилась . А если основание логарифма больше нуля, но меньше единицы, то знак меняется .
Похожие вопросы
Предмет: Алгебра,
автор: manson1231
Предмет: Русский язык,
автор: donerakramov
Предмет: Алгебра,
автор: manson1231
Предмет: Биология,
автор: liza200117
Предмет: Физика,
автор: natalochkakost