алгебра, помогите прошу а


Ответы
Ответ:
В решении.
Объяснение:
1) Решить неравенство (метод интервалов):
х(х - 1/4)(5 + х) < 0
Приравнять к нулю и решить как линейные уравнения:
х₁ = 0;
х - 1/4 = 0
х₂ = 1/4;
5 + х = 0
х₃ = -5.
Отметить найденные корни на числовой прямой:
_______________________________________________________
-∞ - -5 + 0 - 1/4 + +∞
Определить знак самого правого интервала, для этого придать х значение больше 1/4 и подставить в выражение:
х = 1
1(1 - 1/4)(5 + 1) = 4,5 > 0, значит, +.
Проставить знаки на числовой прямой.
Так как неравенство < 0, решения будут в интервалах со знаком -.
Решения неравенства: х∈(-∞; -5)∪(0; 1/4).
Или: x < -5; 0 < x < 1/4. Первый ответ.
Неравенство строгое, скобки круглые.
2) Решить неравенство:
25 - х² > 0
Приравнять к нулю и решить как квадратное уравнение:
25 - х² = 0
-х² = -25/-1
х² = 25
х = ±√25
х = ±5.
График данной функции - парабола, ветви направлены вниз, пересекают ось Ох в точках х = -5 и х = 5. График положителен (неравенство > 0) при х∈(-5; 5).
Решение неравенства: х∈(-5; 5). Ответ 4.
Неравенство строгое, скобки круглые.
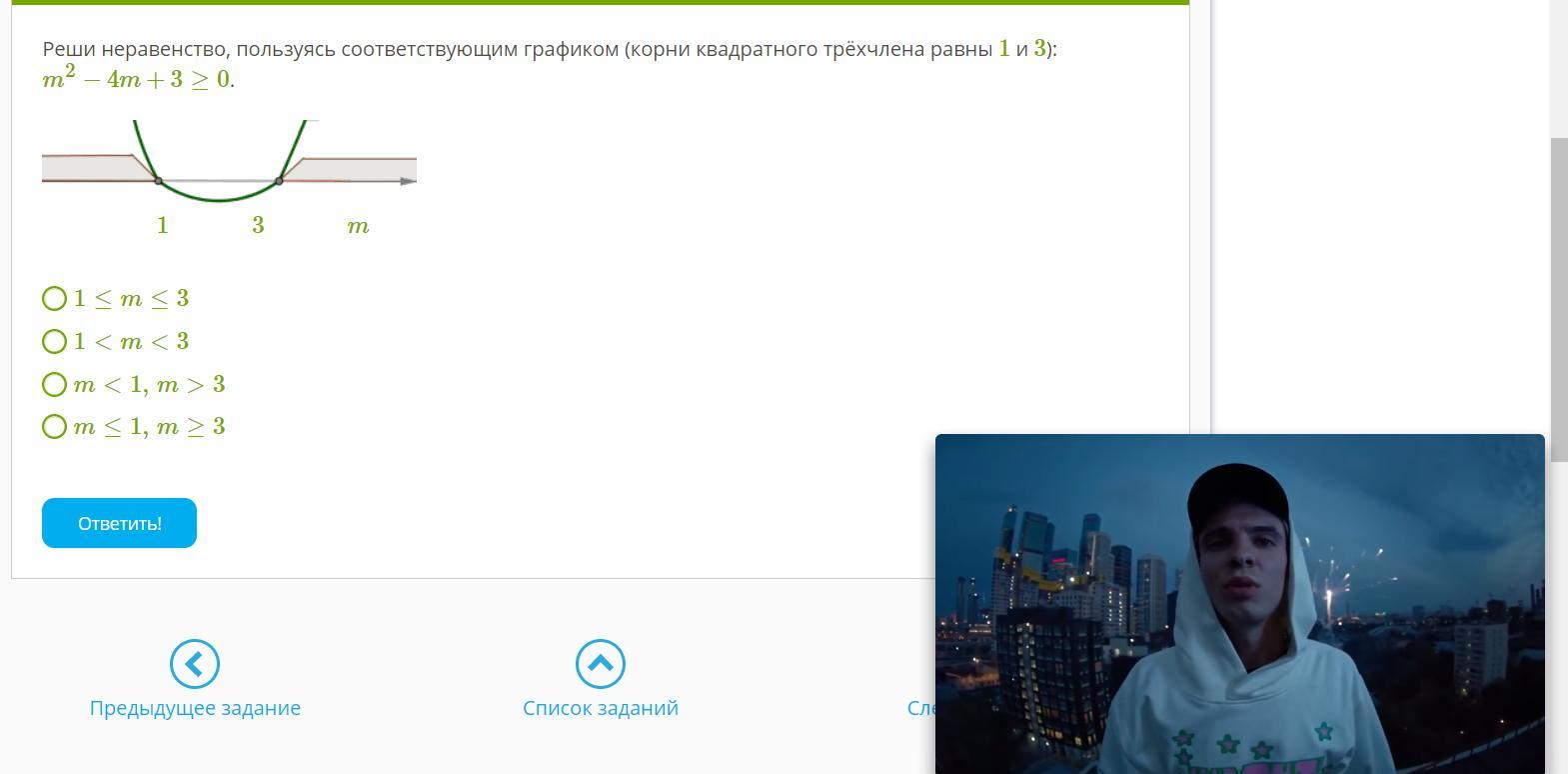
3) Согласно графика, решения неравенства: m <=1; m>=3. Ответ 4.
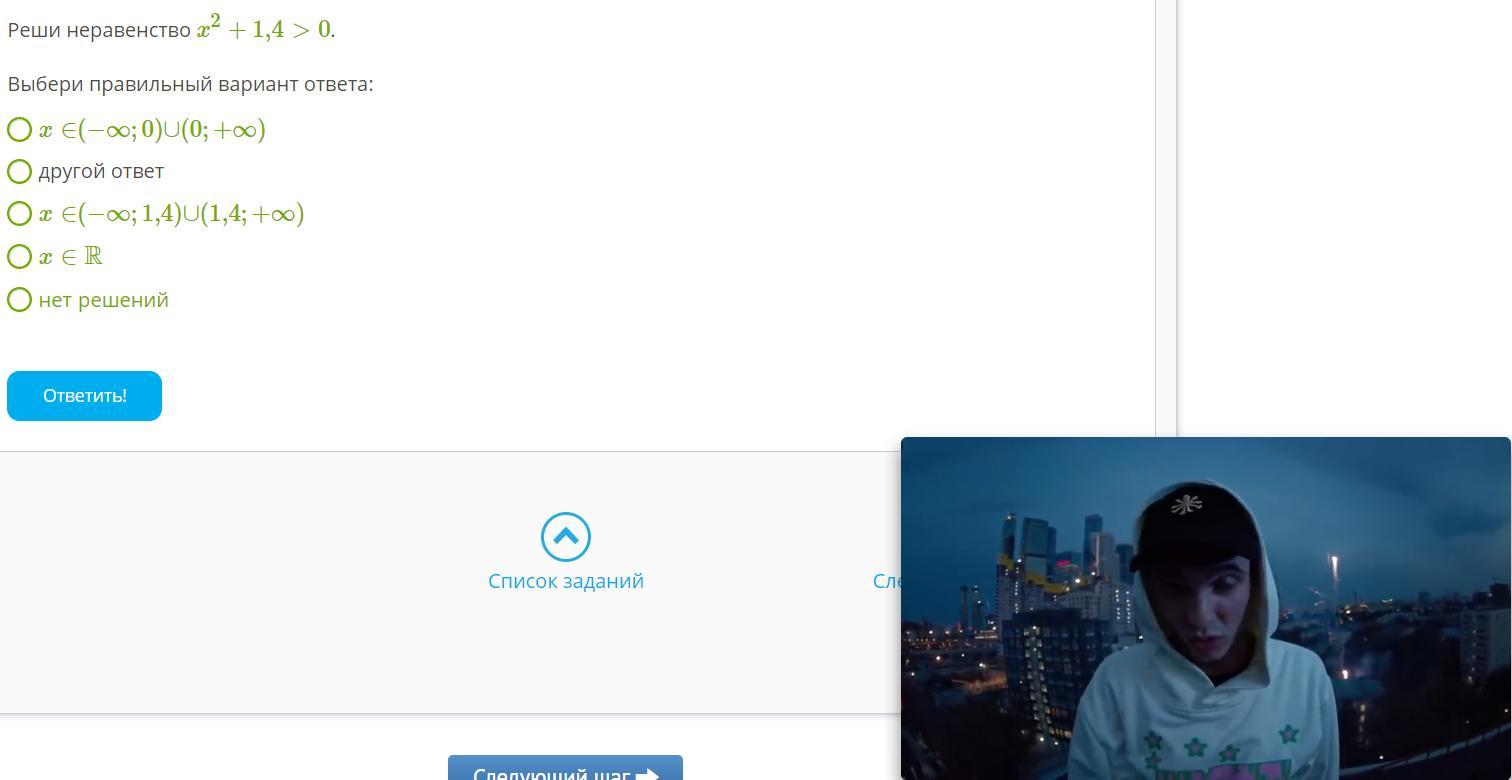
4) Решить неравенство:
х² + 1,4 > 0
Приравнять к нулю и решить как квадратное уравнение:
х² + 1,4 = 0
х² = -1,4
Так как корней уравнения нет, х∈R, или х - любое число. Ответ 4.