Предмет: Алгебра,
автор: Miа16
Алгебра. Даю 10 баллов. Решить 1-4. С подробным объяснением.
Приложения:
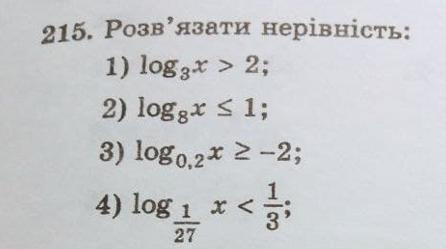
Ответы
Автор ответа:
1
Автор ответа:
1
Объяснение:
ОДЗ: х>0
Ответ: x∈(9;+∞).
ОДЗ: х>0
Ответ: x∈(0;8].
ОДЗ: х>0
Ответ: x∈(0;25].
ОДЗ: х>0
Ответ: x∈(1/3;+∞).
Похожие вопросы
Предмет: Алгебра,
автор: ruha7777
Предмет: Физика,
автор: oagu47mno
Предмет: Алгебра,
автор: Ticci1
Предмет: Українська мова,
автор: marinacikina69
Предмет: Математика,
автор: ostapaldoshin