Предмет: Математика,
автор: 12qwertyu12
МАТАНАЛИЗ!!!!!!!ОЧЕНЬ срочно помогите,пожалуйста,даю 50 баллов!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!Вычислить криволинейный интеграл по замкнутому контуру L
а) непосредственно
б) по формуле Грина
Приложения:
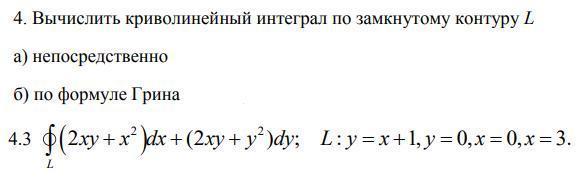
Ответы
Автор ответа:
0
Если нарисовать контур интегрирования, то становится понятно, что исходный интеграл нужно разбить на 4 части под стать получившейся трапеции. Тогда получится следующее:
Все интегралы здесь самые обычные, поэтому подробно я не расписываю.
Аналогичный результат получается и с использование формулы Грина:
Поэтому и, соответственно, искомый интеграл тоже равен 0.
12qwertyu12:
спасибо большое за ответ, но всё же хотелось бы более подробное решение
Похожие вопросы
Предмет: Алгебра,
автор: cmijjey1994
Предмет: Геометрия,
автор: Akita2000
Предмет: Математика,
автор: Аноним
Предмет: Математика,
автор: vika2446