Предмет: Алгебра,
автор: frogg0
НАЙДИТЕ ПОЖАЛУЙСТА ПРОИЗВОДНУЮ
Приложения:
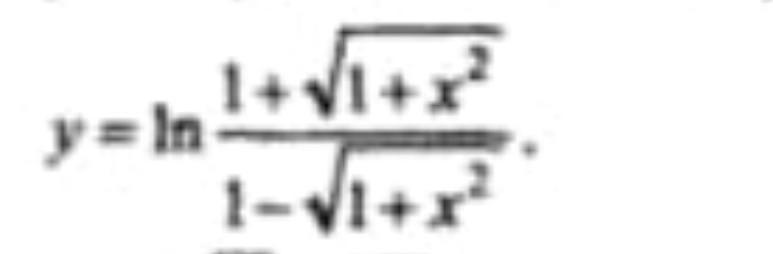
Ответы
Автор ответа:
1
Ответ:
Похожие вопросы
Предмет: Математика,
автор: 90955040Lesa
Предмет: Физика,
автор: dnepro2010
Предмет: Русский язык,
автор: Olga831106
Предмет: Английский язык,
автор: Аноним