Question

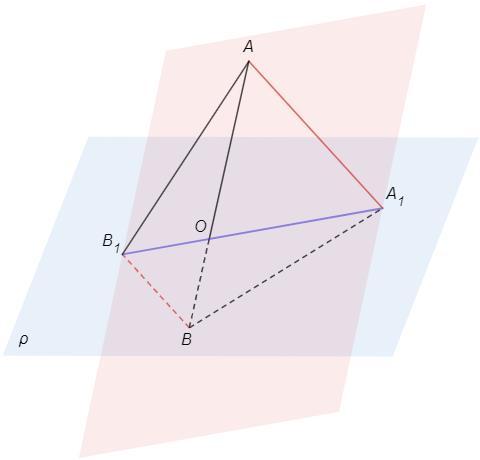
площина p перетинає відрізок AB в точці O, причому AO/OA=2/1.
Через точки А і В проведено паралельні прямі, які перетинають площину p в точках A1 і B1 відповідно. Визначте площу чотирикутника AB1BA1, якщо площа трикутника BOA1, дорівное 5.​

Answer 1

Через две параллельные прямые AA1 и BB1 проходит плоскость.

Плоскости AA1BB1 и p пересекаются по прямой A1B1.

Все общие точки двух плоскостей лежат на этой прямой.

Следовательно точка O лежит на прямой A1B1.

Диагонали трапеции AA1BB1 пересекаются в точке O.

S(BOA1) =S(B1OA) =5

(Это свойство трапеции. Треугольники BAA1 и B1AA1 имеют общее основание и равные высоты (расстояние между параллельными), следовательно их площади равны. Вычитаем общую площадь AOA1

=> S BOA1=S B1OA.)

Треугольники BOA1 и AOA1 имеют общую высоту, следовательно их площади относятся как основания, 1:2.

S(BOA1)/S(AOA1) =1/2 => S(AOA1) =5*2 =10

Аналогично

S(BOB1)/S(B1OA) =1/2 => S(BOB1) =5/2 =2,5

S(AA1BB1) =5 +5 +10 +2,5 =22,5