Через ОДЗ пожалуйста
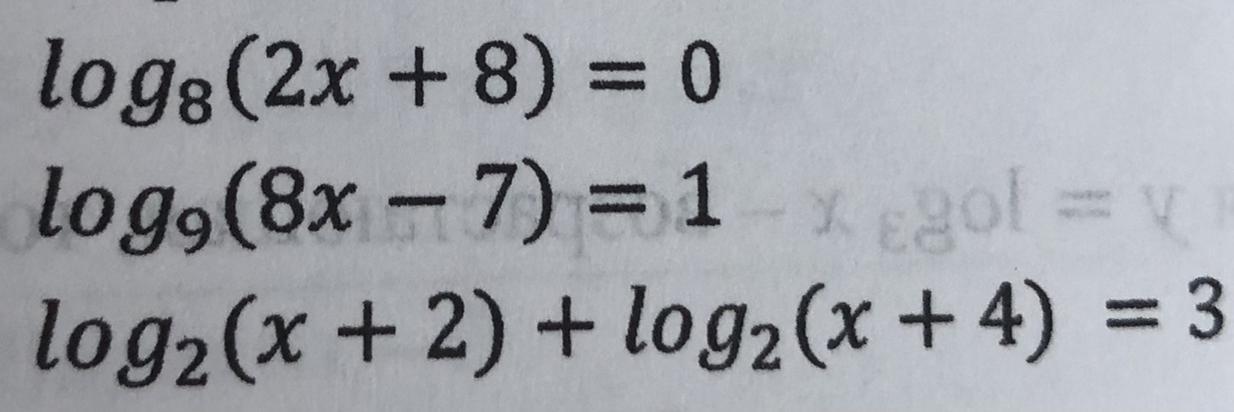
Ответы
Ответ:
) log₃.₂ (2-x) = log₃.₂ (3x+6)
2-x = 3x+6
-4x = 4
x = -1
Ответ: -1
2) log₀.₈(1+2x) = log₀.₈ (4x-10)
1+2x = 4x-10
-2x = -11
x = 5.5
Ответ: 5,5
3) log₂ (x-6) + log₂ (x-8) = 3
ОДЗ: x-6>0
x-8>0
log₂ ((x-6)(x-8)) = log₂8
(x-6)(x-8) = 8
x² - 8x - 6x + 48 = 8
x² - 14x + 40 = 0
D₁ = 49-40 = 9
x₁ = 7+3 = 10
x₂ = 7-3 = 4 не удов. ОДЗ
Ответ: 10
4) log₈ (x-2) - log₈ (x-3) = 1/3
ОДЗ: x-2>0
x-3>0
log₈ ( \frac{x-2}{x-3} )(
x−3
x−2
) = log₈2
\frac{x-2}{x-3}=2
x−3
x−2
=2
x-2 = 2x - 6
-x = -4
x = 4
Ответ: 4
1) lg (5-x) = 1/3 lg(35-x³)
ОДЗ: 5-x>0
35-x³ > 0
lg (5-x) = lg (35- x^{3}) ^{ \frac{1}{3} }(35−x
3
)
3
1
5-x = (35- x^{3}) ^{ \frac{1}{3} }(35−x
3
)
3
1
(5-x)³ = 35-x³
125 - 3*25*x + 3*5*x² - x³ = 35-x³
125 - 75x + 15x² - 35 = 0
15x² - 75x +90 = 0
x² - 5x + 6 = 0
D = 25 - 24 = 1
x₁ = (5+1)/2 = 3
x₂ = (5-1) / 2 =2
Ответ: 3; 2
2) log₂ ( \frac{x-5}{x+5} )(
x+5
x−5
) + log₂ (x+5) = 0
ОДЗ: x-5>0
x+5>0
log₂ (\frac{(x-5)(x+5)}{x+5} )(
x+5
(x−5)(x+5)
) = 0
log₂ (x-5) = 0
x-5 = 1
x = 6
Ответ: 6
3) log₂ (3x-6) - 1 = log₂ (9x-19)
log₂ (3x-6) = log₂ (9x-19) + 1
log₂ (3x-6) = log₂ (9x-19) + log₂2
log₂ (3x-6) = log₂ ((9x-19)*2)
3x-6 = 18x - 38
15x = 32
x = \frac{32}{15}
15
32
Ответ: 32/15
1) log₇ (x-2) +log₇(x+2) = log₇ (4x+41)
ОДЗ: x-2>0
x+2>0
4x+41 >0
log₇ ((x-2)(x+2)) = log₇ (4x+41)
(x-2)(x+2) = 4x+41
x² - 4 = 4x +41
x² - 4x - 45 = 0
D₁ = 4 + 45 = 49
x₁ = 2+7 = 9
x₂ = 2-7 = -5 не удов. ОДЗ
Ответ: 9
2) log₄ (x+1) - log₄(1-x) = log₄ (2x+3)
ОДЗ: x+1>0
1-x>0
2x+3>0
log₄ (x+1) = log₄(2x+3) + log₄ (1-x)
log₄ (x+1) = log₄ ((2x+3)(1-x))
x+1 = 2x - 2x² + 3 - 3x
2x² + 2x - 2 = 0
x² + x - 1 = 0
D = 1 + 4 = 5
x₁ = (-1+√5)/2
x₂ = (-1-√5) / 2 не удов.ОДЗ
Ответ: (-1+√5) / 2
3) log₄ (x+3) - log₄ (x-1) = 2- log₄8
log₄ (\frac{x+3}{x-1}) =(
x−1
x+3
)= log₄16 - log₄8
log₄ ( \frac{x+3}{x-1})(
x−1
x+3
) = log₄2
(\frac{x+3}{x-1}) = 2
x−1
x+3
)=2
x+3 = 2x - 2
-x = -5
x = 5
Ответ: 5
4) lg (x-1) + lg (x+1) = 3lg2 + lg (x-2)
lg ((x-1)(x+1)) = lg8 + lg (x-2)
lg (x² - 1) = lg (8(x-2))
x² - 1 = 8x- 16
x² - 8x + 15 = 0
D₁ = 16 - 15 = 1
x₁ = 4 + 1 =5
x₂ = 4-1 = 3
Ответ: 5;3
1) 2log₃(x-2) + log₃ (x-4)² = 0
ОДЗ: x-2>0
x-4>0
2log₃ (x-2)+ 2log₃ (x-4) = 0
2 (log₃(x-2) + log₃ (x-4)) = 0
log₃ ((x-2)(x-4)) = 0
(x-2)(x-4) = 1
x² - 4x - 2x + 8 = 1
x² - 6x + 7 = 0
D₁ = 9 - 7 = 2
x₁ = 3 + √2
x₂ = 3 -√2 не удов. ОДЗ
Ответ; 3+√2
2) 2lgx - lg4 + lg (5-x²) = 0
ОДЗ: x>0
5-x² > 0
lgx² + lg (5-x²) = lg4
lg (x² (5-x²)) = lg4
x² (5-x²) = 4
5x² - x⁴ = 4
5x² - x⁴ - 4 = 0
x⁴ - 5x² + 4 =0
x² = t ; t>0
t² - 5t + 4 = 0
t₁ = 1
t₂ = 4
x² = 1 x² = 4
x₁ = 1 x₁ = 2
x₂ = -1 x₂ = -2
корни -1 и -2 не удов. ОДЗ
Ответ: 1; 2