Question

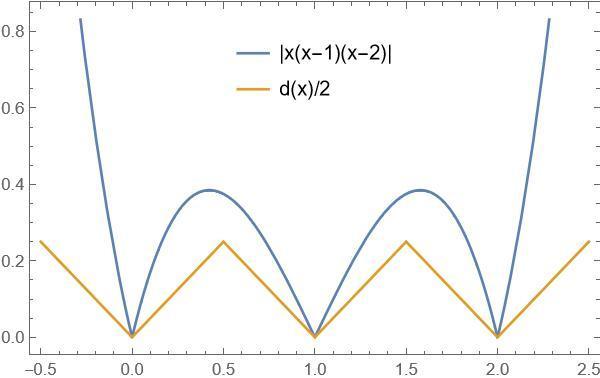
|x(x-1)(x-2)|>=d(x)/2

Где d(x) это расстояние от x до ближайшего целого числа.

Докажите, что это неравенство верно для любого x

Answer 1

Самое проблемное место этой задачи - найти явный вид функции $d(x)$

Немного подумав, несложно заметить, что целые числа идут друг за другом с шагом в единицу, а значит любое действительное число отстоит от ближайшего целого не более чем на 0.5 и не менее чем на 0.

Понятно, что $d(x)$ должна быть периодической, коль целые числа встречаются с перидом 1. Нарисовав эту зависимость для, например, всех $x$ из [0, 1], мы "повторением" можем получить искомую $d(x)$. Видно, что это обычный модуль:

$d(x) = \frac{1}{2} -|x-(k+\frac{1}{2})|$  где $x \in [k, k+1]$ и $k \in \mathbb{Z}$

Теперь, когда известен вид $d(x)$, все остальные операции превращаются в типичное сравнение двух функций на разных интервалах. Больше всего внимания нужно уделить небольшой окрестности, в которой расположены нули полинома $x(x-1)(x-2)$. Она как раз и нарисована на графике в прекрепленных файлах.

Рассмотрю лишь один один интервал, остальные делаются аналогично.

Пусть $x \in [0, 0.5]$, тогда $|x(x-1)(x-2)| \ge d(x)/2$ эквивалентно

$x(x-1)(x-2) \ge \frac{x}{2}$

$x(2x^2-6x+3) \ge 0$

$x \left(x+\frac{1}{2} \left(-3-\sqrt{3}\right)\right) \left(x+\frac{1}{2} \left(\sqrt{3}-3\right)\right)\geq 0$

что справедливо для всех $x \in [0, 0.5]$

Проверив похожие неравенства для прочих интервалов, мы тем самым решим задачу.