Question

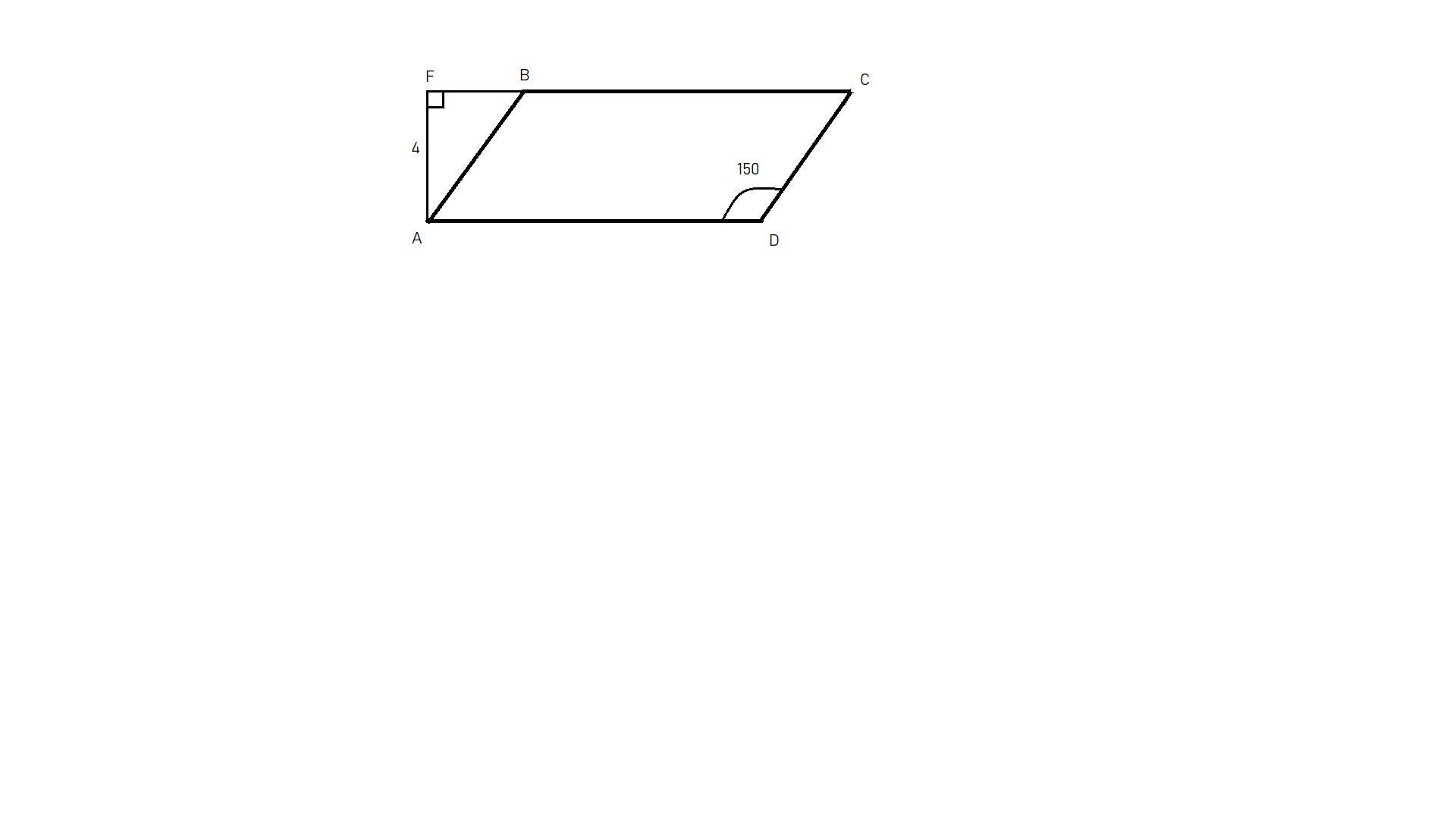
Из вершины угла А параллелогиамма ABCD проведена высота параллелограмма AF, длина которой равна 4 см. Найдите стороны параллелограмма, если угол ADC=150°, а периметр параллелограмма равен 28 см

Answer 1

Ответ:

Объяснение:

Чертеж на фото.

Т.к ABCD-параллелограмм, ∠АDС=∠АBС=150°, тогда ∠BAD=∠DCB=180-150=30°.

∠BAD=ABF=30°(т.к. углы накрест лежащие)

ΔAFB-прямоугольный, ∠AFB=90°,∠ABF=30°, по свойству углов прямоугольного треугольника, катет, лежащий против угла в 30° равен половине гипотенузы, значит AB=2AF=4*2=8см

AB=CD=8 см, т.к. ABCD-параллелограмм.

P(ABCD)=AB+CD+AD+BC.

Неизвестные стороны AD и BC примем за х( они равны. т.к. ABCD-параллелограмм)

28=8+8+х+х

2х+16=28

2х=28-16

2х=12

х=6см-AD и BC

Ответ:8см, 8см, 6см, 6см.