Question

алгебра даю 100 баллов

Answer 1

Ответ:

Объяснение:

$\displaystyle\bf\left \{ {{x^2-2y>7} \atop {3x+y>3}} \right.$

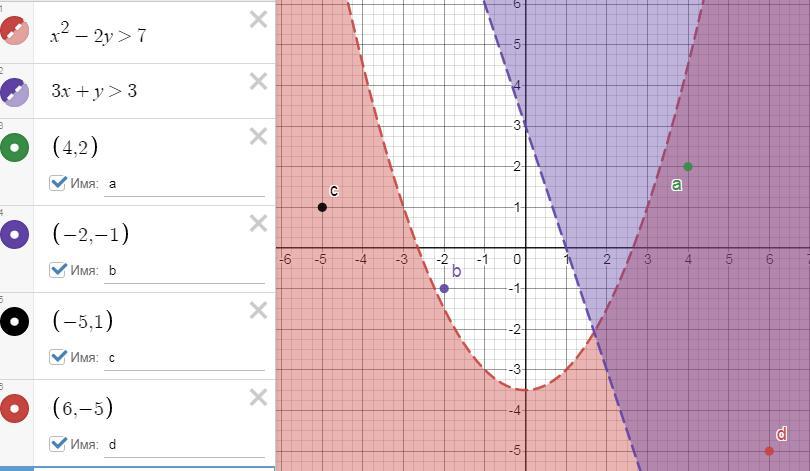
проверим, являются ли пары чисел решением

системы неравенств

a) (4;2)

x=4; y=2

4²-2·2=16-4=12>7  верно

3·4+2=12+2=14>3 верно

пара (4;2) является решением системы неравенств

b) (-2;-1)

x=-2; y=-1

(-2)²-2·(-1)=4+2=6>7  неверно

пара (-2;-1) не является решением системы неравенств

с) (-5;1)

x=-5; y=1

(-5)²-2·1=25-2=23>7  верно

3·(-5)+1=-15+1=-14>3  неверно

пара (-5;1) не является решением системы неравенств

d) (6;-5)

x=6; y=-5

6²-2·(-5)=36+10=46>7  верно

3·6-5=18-5=13>3    верно

пара (6;-5) является решением системы неравенств

Ответ: a) (4;2)    d) (6;-5)