Question

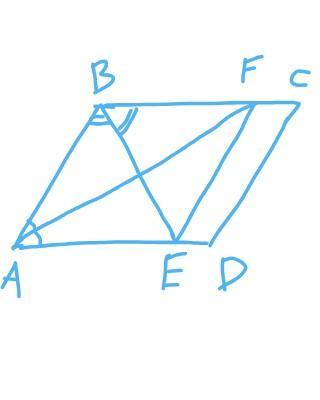
Бісектриси кутів А і В паралелограма ABCD перетинають
його сторони BC і AD у точках F i Е відповідно. Визначте
вид чотирикутника ABFE.

Answer 1

Биссектриса параллелограмма отсекает от него равнобедренный треугольник, это свойство параллелограмма =>

AF — биссектрисса, треуг. ABF — равнобедренный, AB = BF,

BE — биссектриса, треуг. ABE — равнобедренный, AB = AE,

=> AB = BF = AE.

Противоположные стороны параллелограмма попарно параллельны, BC || AD => BF || AE,

Если BF = AE и BF || AE, то и AB = FE, AB || FE.

Получился четырехугольник ABFE, у которого все стороны равны, а противоположные стороны попарно параллельны. Это ромб.

Параллелограм — четырехугольник, у которого противоположные стороны попарно параллельны, Ромб — параллелограм, у которого все стороны равны.