Предмет: Математика,
автор: yulechkavorobeva2021
Найти предел лим принадлежит 1...
Приложения:
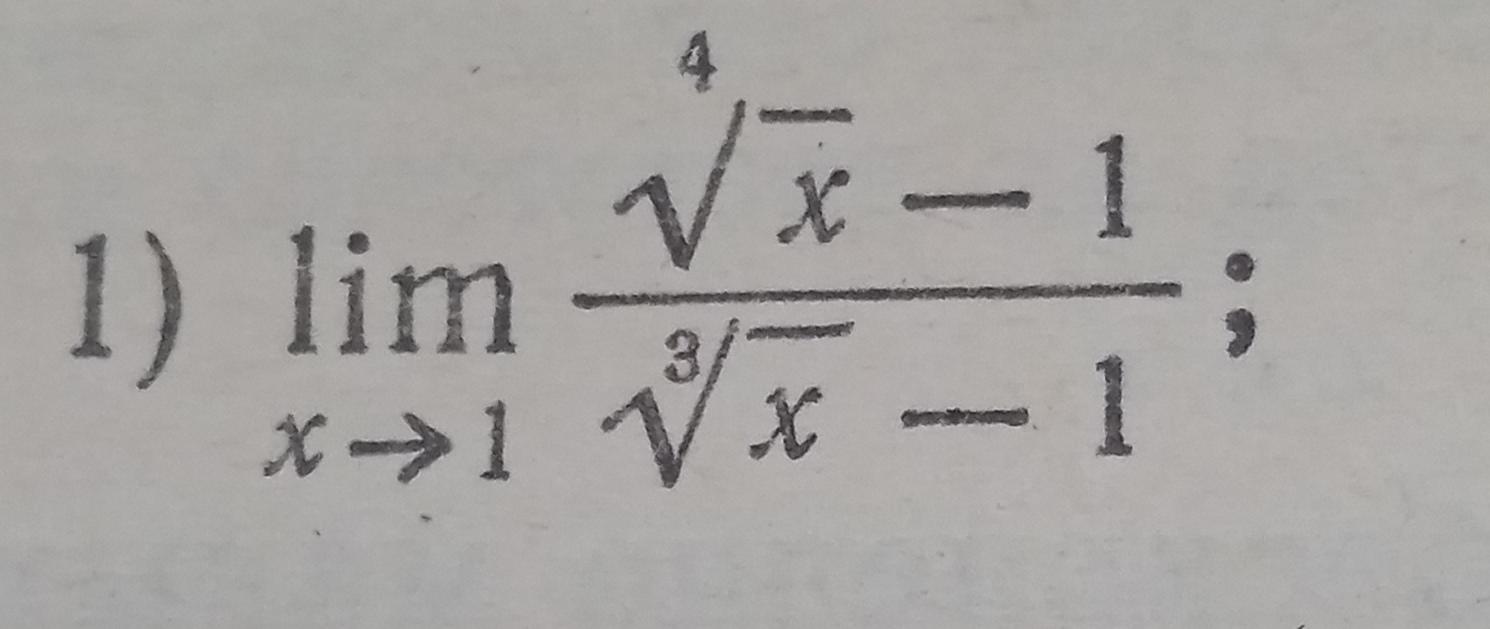
Ответы
Автор ответа:
1
по идее надо как то сократить х - 1
неохота брать производные
a³ - b³ = (a - b)(a² + ab + b²)
a² - b² = (a - b)(a + b)
-----
проводим преобразования
1/(∛x - 1) и ⁴√x - 1 доводим до х - 1
работаем со знаменателем
1/(∛x - 1) = (∛x² + ∛x + 1) / (∛x - 1)(∛x² + ∛x + 1) = (∛x² + ∛x + 1) / (x - 1)
С числителем
⁴√x - 1 = (⁴√x - 1)(⁴√x + 1)/(⁴√x + 1) = (√x - 1)/(⁴√x + 1) = (√x - 1)*(√x + 1)/(⁴√x + 1)(√x + 1) = (x - 1) / (⁴√x + 1)(√x + 1)
итак
lim(x->1) (⁴√x - 1)/(∛x - 1) = lim(x->1) (∛x² + ∛x + 1) / (x - 1) * (x - 1) / (⁴√x + 1)(√x + 1) = lim(x->1) (∛x² + ∛x + 1) / (⁴√x + 1)(√x + 1) = (∛1² + ∛1 + 1) / (⁴√1 + 1)(√1 + 1) = (1 + 1 + 1)/(1 + 1)(1 + 1) = 3/4
yulechkavorobeva2021:
Спасибо большое!!!
Похожие вопросы
Предмет: Русский язык,
автор: азнив
Предмет: Алгебра,
автор: mosg
Предмет: Математика,
автор: artem20005
Предмет: Литература,
автор: daryna2003voloshuna
Предмет: Математика,
автор: Аноним